
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=![]() (x>0)相交于P(1,m).
(x>0)相交于P(1,m).
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( );
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.

【答案】(1)k=1;(2)(2,1);(3)抛物线解析式为:y=﹣![]() x2+x+
x2+x+![]() ,对称轴方程为x=
,对称轴方程为x=![]() .
.
【解析】试题分析:(1)直接将![]() 点代入反比例函数解析式得出
点代入反比例函数解析式得出![]() 的值,进而把
的值,进而把![]() 点代入一次函数解析式得出答案;
点代入一次函数解析式得出答案;
(2)利用全等三角形的判定和性质得出![]() 即可得出
即可得出![]() 点坐标;
点坐标;
(3)直接利用待定系数法求出二次函数解析式进而得出答案.
试题解析: (1)把P(1,m)代入![]() 得m=2,
得m=2,
∴P(1,2)
把(1,2)代入y=kx+1,得k=1;
(2)如图所示:过点P作PA⊥y轴于点A,过点Q作QB⊥x轴于点B,
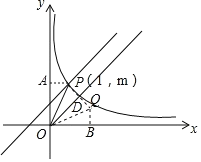
∵点Q与点P关于y=x成轴对称,OP=OQ,
![]()
∴∠AOP=∠BOQ,
在△APO和△BQO中,
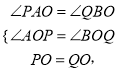
![]()
∴AO=OB=2,AP=QB=1,
∴Q点的坐标为:(2,1).
故答案为:(2,1);
(3)设抛物线的解析式为![]() 得:
得:
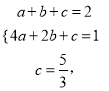 解得
解得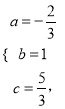
故抛物线解析式为: ![]()
则对称轴方程为


科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”, 3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:

(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作矩形”的尺规作图过程,已知:![]()
求作:矩形![]()
作法:如图,
①作线段![]() 的垂直平分线角交
的垂直平分线角交![]() 于点
于点![]() ;
;
②连接![]() 并延长,在延长线上截取
并延长,在延长线上截取![]()
③连接![]()
所以四边形![]() 即为所求作的矩形
即为所求作的矩形
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:![]() ,
,![]() ,
,
![]() 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)
![]()
![]() 四边形
四边形![]() 是矩形( )(填推理的依据)
是矩形( )(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com