
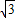 ,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处.
,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处. 时,过点A作AM⊥PD于点M,若k=
时,过点A作AM⊥PD于点M,若k= ,求证:二次函数y=-2x2-(7k-3
,求证:二次函数y=-2x2-(7k-3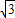 )x+
)x+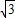 k的图象关于y轴对称.
k的图象关于y轴对称.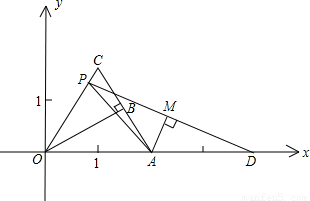
 ,∠OBA=90,解直角△OAB可知∠OAB=60°,由折叠可知∠C=∠OAB=60°,故△OAC为等边三角形;
,∠OBA=90,解直角△OAB可知∠OAB=60°,由折叠可知∠C=∠OAB=60°,故△OAC为等边三角形; 时,可求线段PE、OE、ED及△PAD的面积,用勾股定理可求PD的长,用面积法可求AM长,从而可求k值,就能确定抛物线解析式了,也就能回答问题了.
时,可求线段PE、OE、ED及△PAD的面积,用勾股定理可求PD的长,用面积法可求AM长,从而可求k值,就能确定抛物线解析式了,也就能回答问题了.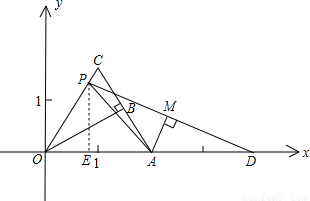 (1)证明:由题意可知OA=OC,
(1)证明:由题意可知OA=OC, ,A的坐标为(2,0)
,A的坐标为(2,0)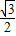
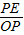
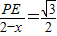
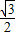 (2-x)=-
(2-x)=-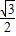 x+
x+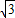
 AD•PE=
AD•PE= (4-2)•PE=PE
(4-2)•PE=PE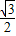 x+
x+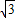 ;
; 时,即PC=
时,即PC=

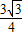

 =
=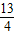
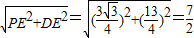
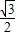 x+
x+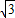 =-
=-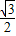 •
• +
+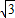 =
=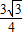
 PD•AM=
PD•AM=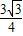
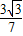 ,
,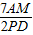 =
=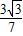
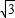 )x+
)x+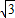 k=-2x2-(7×
k=-2x2-(7×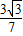 -3
-3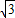 )x+
)x+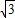 ×
×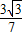



 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
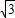 ,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处.
,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处. 时,过点A作AM⊥PD于点M,若k=
时,过点A作AM⊥PD于点M,若k=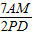 ,求证:二次函数y=-2x2-(7k-3
,求证:二次函数y=-2x2-(7k-3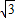 )x+
)x+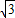 k的图象关于y轴对称.
k的图象关于y轴对称.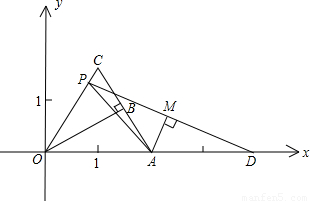
查看答案和解析>>
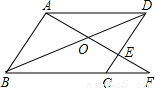
科目:初中数学 来源:2001年全国中考数学试题汇编《四边形》(01)(解析版) 题型:选择题
查看答案和解析>>
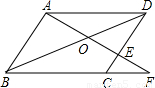
科目:初中数学 来源:2009年全国中考数学试题汇编《图形的相似》(01)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《三角形》(06)(解析版) 题型:填空题
 ),点C在坐标平面内.若以A,B,C为顶点构成的三角形是等腰三角形,且底角为30°,则满足条件的点C有 个.
),点C在坐标平面内.若以A,B,C为顶点构成的三角形是等腰三角形,且底角为30°,则满足条件的点C有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com