
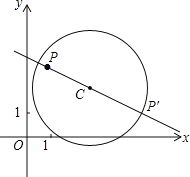
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.
(1)当⊙O的半径为1时.
①分别判断点M(3,4),N(![]() ,0),T(1,
,0),T(1,![]() )关于⊙O的限距点是否存在?若存在,求其坐标;
)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.
问题1:若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,则r的最小值为__________.
问题2:若点P关于⊙C的限距点P′不存在,则r的取值范围为_________.
【答案】(1)①点M、点T关于⊙O的限距点不存在,点N关于⊙0的限距点存在,坐标为(1,0);②﹣1≤x≤﹣![]() 或x=1;(2)问题1:
或x=1;(2)问题1:![]() ;问题2:0<r<
;问题2:0<r<![]() .
.
【解析】
(1)①根据限距点的定义即可判断.
②分三种情形:①当点P在线段EF上时,②当点P在线段DE、DF(不包括端点)上时,③当点P与点D重合时,分别说明即可解决问题.
(2)问题1:如图2中,△PP′C是等边三角形,点P在PP′上运动时,有限距点,列出不等式即可解决.
问题2:如图2中,当点H不存在限距点时,点P就不存在限距点,列出不等式即可解决.
解:(1)①如图

![]() M(3,4),N(
M(3,4),N(![]() ,0),T(1,
,0),T(1,![]() )
)
![]()
当⊙O的半径为1时即![]()
![]() ,点M的限距点不存在;
,点M的限距点不存在;
![]() ,点T的限距点不存在;
,点T的限距点不存在;
![]() ,
,![]() ,点N的限距点存在即为
,点N的限距点存在即为![]()
所以点M、点T关于⊙O的限距点不存在,点N关于⊙O的限距点存在,坐标为(1,0).
②∵点D坐标为(2,0),⊙O半径为1,DE、DF分别切⊙O于E、F,
![]()
![]()
![]()
![]()
![]()
由对称可得F(![]() ,﹣
,﹣![]() )
)
∴切点坐标为(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ),
),
如图所示,不妨设点E(![]() ,
,![]() ),点F(
),点F(![]() ,﹣
,﹣![]() ),EO、FO的延长线分别交⊙O于点E′、F′,则E′(﹣
),EO、FO的延长线分别交⊙O于点E′、F′,则E′(﹣![]() ,﹣
,﹣![]() ),F′(﹣
),F′(﹣![]() ,
,![]() ).
).
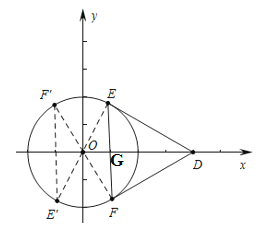
设点P关于⊙O的限距点的横坐标为x,
①当点P在线段EF上时,直线PO与⊙O的交点P′满足1≤PP′≤2,故点P关于⊙O的限距点存在,其横坐标x满足﹣1≤x≤﹣![]() .
.
②当点P在线段DE、DF(不包括端点)上时,直线PO与⊙O的交点P′满足0<PP′<1或2<PP′<3,故点P关于⊙O的限距点不存在.
③当点P与点D重合时,直线PO与⊙O的交点P′(1,0),满足PP′=1,故点P关于⊙O的限距点存在,其横坐标x=1.
综上所述点P关于⊙O的限距点的横坐标x的范围为﹣1≤x≤﹣![]() 或x=1.
或x=1.
(2)问题1:如图中,

∵△DEF是等边三角形,点C是△DEF的外接圆的圆心,
∵若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,
∴图中△PP′C是等边三角形,点P在PP′上运动时,有限距点,
∵PC∥ED,
∴![]() =
=![]() =
=![]() ,
,
∴PC=![]() ,
,
由题意:r≤![]() ﹣r≤2r,
﹣r≤2r,
∴![]() ,
,
∴r的最小值为![]() .
.
问题2:如图中,当点H不存在限距点时,点P就不存在限距点,

∵HC=![]() ,
,
∴![]() ﹣r>2r,
﹣r>2r,
∴r<![]() ,
,
∴0<r<![]() 时点P的限距点不存在.
时点P的限距点不存在.
故答案分别为![]() ,0<r<
,0<r<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
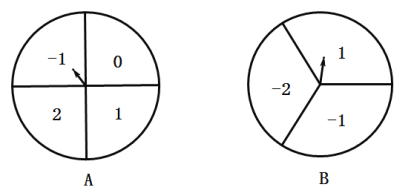
(1)画树状图或列表求出各人获胜的概率。
(2)这个游戏公平吗?说说你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=![]() (x<0)经过点C.
(x<0)经过点C.
(1)m的取值范围是 ;
(2)若点B(﹣1,1),判断双曲线是否经过点A;
(3)设点B(a,2a+1).
①若双曲线经过点A,求a的值;
②若直线y=2x+2交AB于点E,双曲线与线段AE有交点,求a的取值范围.
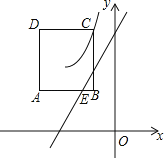
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为60°”的尺规作图过程
已知:⊙O
求作:矩形ABCD,使得矩形ABCD内接于⊙O,且其对角线AC,BD的夹角为60°.
作法:如图
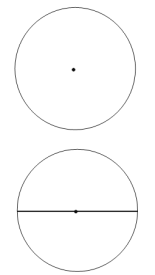
①作⊙O的直径AC;
②以点A为圆心,AO长为半径画弧,交直线AC上方的圆弧于点B;
③连接BO并延长交⊙O于点D;
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点A,C都在⊙O上,
∴OA=OC
同理OB=OD
∴四边形ABCD是平行四边形
∵AC是⊙O的直径,
∴∠ABC=90° ( )(填推理的依据)
∴四边形ABCD是矩形
∵AB= =BO,
∴四边形ABCD四所求作的矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为多少?
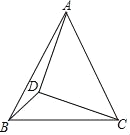
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() .(1)已知点
.(1)已知点![]() 在第一象限的抛物线上,则点
在第一象限的抛物线上,则点![]() 的坐标是_______.(2)在(l)的条件下连接
的坐标是_______.(2)在(l)的条件下连接![]() ,
,![]() 为抛物线上一点且
为抛物线上一点且![]()
![]() ,则点
,则点![]() 的坐标是_______.
的坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
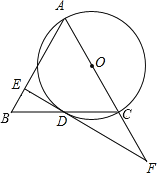
【题目】如图,以等腰△ABC的一腰AC为直径作⊙O,交底边BC于点D,过点D作腰AB的垂线,垂足为E,交AC的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)证明:∠CAD=∠CDF;
(3)若∠F=30°,AD=![]() ,求⊙O的面积.
,求⊙O的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com