
【题目】某商品的进价为每件![]() 元,现在的售价为每件
元,现在的售价为每件![]() 元,每星期可卖出
元,每星期可卖出![]() 件.市场调查反映:如果每件售价每涨
件.市场调查反映:如果每件售价每涨![]() 元(售价每件不能高于
元(售价每件不能高于![]() 元),那么每星期少卖
元),那么每星期少卖![]() 件.设每件售价为
件.设每件售价为![]() 元(
元(![]() 为非负整数),则若要使每星期的利润最大且每星期的销量较大,
为非负整数),则若要使每星期的利润最大且每星期的销量较大,![]() 应为多少元?( )
应为多少元?( )
A. 41 B. 42 C. 42.5 D. 43
【答案】B
【解析】
售价为x元,则涨价为(x-40)元,可用x表示出每星期的销量,并得到x的取值范围.根据总利润=销量×每件利润可得出利润的表达式,利用二次函数的最值可得出答案.
解:由题意得,涨价为(x-40)元,(0≤x≤5且x为整数),每星期少卖10(x-40)件,
∴每星期的销量为:150-10(x-40)=550-10x,
设每星期的利润为y元,
则y=(x-30)×(550-10x)=-10(x-42.5)2+1562.5,
∵x为非负整数,
∴当x=42或43时,利润最大为1560元,
又∵要求销量较大,
∴x取42元.
答:若要使每星期的利润最大且每星期的销量较大,x应为42元.
故选:B.


科目:初中数学 来源: 题型:
【题目】己知二次函数![]() 中,函数
中,函数![]() 与自变量
与自变量![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
| 0 | 1 | 2 | 3 | 4 | … |
| … | 10 | 5 | 2 | 1 | 2 | 5 | … |
(1)求该二次函数的解析式;
(2)当![]() 为何值时,
为何值时,![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若![]() ,
,![]() 两点都在该函数的图像上,试比较
两点都在该函数的图像上,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)=![]() .
.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点![]() 和
和![]() 、点
、点![]() 和
和![]() 分别关于
分别关于![]() 轴对称,隧道拱部分
轴对称,隧道拱部分![]() 为一条抛物线,最高点
为一条抛物线,最高点![]() 离路面
离路面![]() 的距离为
的距离为![]() 米,点
米,点![]() 离路面为
离路面为![]() 米,隧道的宽度
米,隧道的宽度![]() 为
为![]() 米;则隧道拱抛物线
米;则隧道拱抛物线![]() 的函数解析式________.
的函数解析式________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字并填空:数学课上张老师出了这样一道题:“如图,在![]() 中,
中,![]() ,
,![]() 是中线,点
是中线,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .求证:
.求证:![]() ”
”

张老师给出了如下简要“要证![]() ,就是要证线段的倍分问题,所以有两个思路,思路一:找
,就是要证线段的倍分问题,所以有两个思路,思路一:找![]() ,故取
,故取![]() 的中点
的中点![]() ,连接
,连接![]() ,只要证
,只要证![]() 即可.这就将证明线段倍分问题______为证明线段相等问题,只要证出______,则结论成立.思路二:变
即可.这就将证明线段倍分问题______为证明线段相等问题,只要证出______,则结论成立.思路二:变![]() 为
为![]() ,因为需要找到
,因为需要找到![]() ,于是延长
,于是延长![]() 至点
至点![]() ,使
,使![]() ,只要证______即可.连接
,只要证______即可.连接![]() ,若证出______
,若证出______![]() ______则结论成立.”你认为在现阶段可以用思路______来完成这个证明.
______则结论成立.”你认为在现阶段可以用思路______来完成这个证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
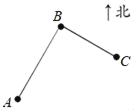
A. 6000米 B. 5000米 C. 4000米 D. 2000米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com