
【题目】如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=![]() ,弦BM平分∠ABC交AC于点D,连接MA,MC.
,弦BM平分∠ABC交AC于点D,连接MA,MC.
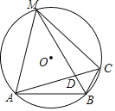
(1)试判断![]() 的形状;
的形状;
(2)求⊙O半径的长.
【答案】(1)等边三角形;(2)2.
【解析】
(1)由角平分线的性质可得∠ABM=∠CBM=60°,根据等弧对等角可得∠MAC=∠MBC=60°, ∠MCA=∠MBA=60°,进而可得![]() 为等边三角形;
为等边三角形;
(2)过点O作OH⊥AC于H,连接AO,CO,易知∠AOC=2∠AMC=120°,由垂径定理可得∠AOH=60°,AH=![]() ,然后解直角三角形可得AO的长度.
,然后解直角三角形可得AO的长度.
(1)∵∠ABC=120°,弦BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∴∠MAC=∠MBC=60°, ∠MCA=∠MBA=60°,
∴![]() 为等边三角形;
为等边三角形;
(2)过点O作OH⊥AC于H,连接AO,CO.
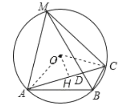
∵![]() 为等边三角形
为等边三角形
∴∠AMC=60°,
∴∠AOC=2∠AMC=120°,
∵OH⊥AC,OA=OC,
∴∠AOH=60°,AH=![]() AC=
AC=![]() ,
,
在![]() 中,sin∠AOH=
中,sin∠AOH=![]()
∴AO=![]() =
=![]() =2,
=2,
∴⊙O的半径为2.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂
的等腰直角三角形,摆动臂![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
(1)在旋转过程中,当![]() 为同一直角三角形的顶点时,
为同一直角三角形的顶点时,![]() 的长为______________.
的长为______________.
(2)若摆动臂![]() 顺时针旋转90°,点
顺时针旋转90°,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,
,![]() 的长为______________.
的长为______________.
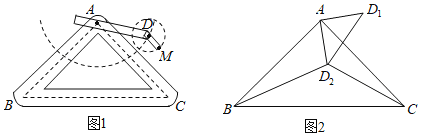
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,过点
,过点![]() 三点的
三点的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]()
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题
,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题

查看答案和解析>>
科目:初中数学 来源: 题型:
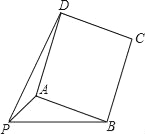
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽度为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540 m2 , 求道路的宽.如果设小路宽为x m,根据题意,所列方程正确的是( )
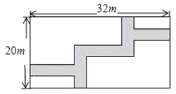
A.(20+x)(32+x)=540
B.(20﹣x)(32﹣x)=100
C.(20﹣x)(32﹣x)=540
D.(20-2x)(32﹣2x)=540
查看答案和解析>>
科目:初中数学 来源: 题型:
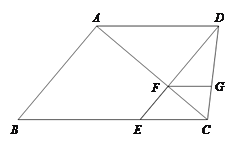
【题目】已知:如图,梯形ABCD中,AD∥BC,DE∥AB,![]() 与对角线
与对角线![]() 交于点
交于点![]() ,
,![]() ∥
∥![]() ,且FG=EF.
,且FG=EF.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)联结AE,又知AC⊥ED,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,与y轴相交于点C,顶点为P.
,与y轴相交于点C,顶点为P.
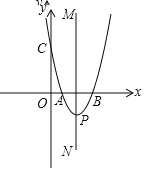
(1)求这条抛物线的表达式和顶点P的坐标;
(2)点E在抛物线的对称轴上,且![]() ,求点E的坐标;
,求点E的坐标;
(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com