解:(1)∵AB是⊙O的直径,OD=5,
∴∠ADB=90°,AB=10,
在Rt△ABD中,sin∠BAD=

,sin∠BAD=

,
∴
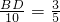
,BD=6,
∴AD=
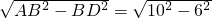
=8,
∵∠ADB=90°,AB⊥CD,
∴DE•AB=AD•BD,CE=DE,
∴DE×10=8×6,
∴DE=

∴CD=2DE=

;
(2)∵AB是⊙O的直径,AB⊥CD,
∴
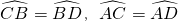
,
∴∠BAD=∠CDB,∠AOC=∠AOD,
∵AO=DO,
∴∠BAD=∠ADO,
∴∠CDB=∠ADO,
设∠ADO=4x,则∠CDB=4x.
由∠ADO:∠EDO=4:1,则∠EDO=x.
∵∠ADO+∠EDB+∠EDO=90°,
∴4x+4x+x=90°,
解得:x=10°,
∴∠AOD=180°-(∠OAD+∠ADO)=100°,
∴∠AOC=∠AOD=100°,
∴S
扇形OAC=
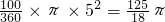
.
分析:(1)首先根据锐角三角函数求得直角三角形ABC的两条直角边,再根据面积计算其斜边上的高,进一步根据垂径定理计算弦长;
(2)根据直角三角形的两个锐角互余结合已知条件求得扇形所对的圆心角,进一步求其面积.
点评:本题为圆的综合题,综合考查了解直角三角形、三角函数、阴影部分面积等相关知识.

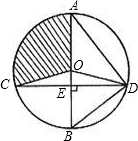 如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5. ,求CD的长;
,求CD的长; ,sin∠BAD=
,sin∠BAD= ,
,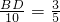 ,BD=6,
,BD=6,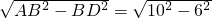 =8,
=8,
 ;
;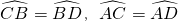 ,
,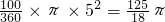 .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案