
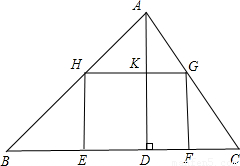
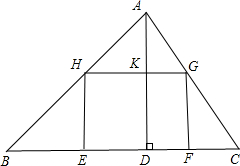 鄂州市圆梦园别墅区有一块三角形ABC的空地,BC=30米,BC边上的高AD=20米,现计划在这块空地上修建一个矩形游泳池EFGH,使EF在BC边上,H、G分别在AB,BC边上,设EH为x米,矩形的面积为S.
鄂州市圆梦园别墅区有一块三角形ABC的空地,BC=30米,BC边上的高AD=20米,现计划在这块空地上修建一个矩形游泳池EFGH,使EF在BC边上,H、G分别在AB,BC边上,设EH为x米,矩形的面积为S.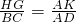 ,
, =
=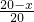 ,
, ×(-1.5x+30)×(20-x)×80=60x2-2400x+24000,
×(-1.5x+30)×(20-x)×80=60x2-2400x+24000, -(-1.5x2+30x+
-(-1.5x2+30x+ x2-30x+300)]×40=30x2,
x2-30x+300)]×40=30x2,

科目:初中数学 来源: 题型:
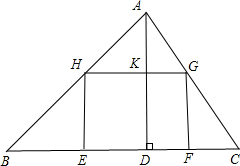 鄂州市圆梦园别墅区有一块三角形ABC的空地,BC=30米,BC边上的高AD=20米,现计划在这块空地上修建一个矩形游泳池EFGH,使EF在BC边上,H、G分别在AB,BC边上,设EH为x米,矩形的面积为S.
鄂州市圆梦园别墅区有一块三角形ABC的空地,BC=30米,BC边上的高AD=20米,现计划在这块空地上修建一个矩形游泳池EFGH,使EF在BC边上,H、G分别在AB,BC边上,设EH为x米,矩形的面积为S.查看答案和解析>>
科目:初中数学 来源:2011年3月湖北省鄂州市鄂城区燕矶中学九年级(下)月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com