Question

平面直角坐标系中,M(36,0),⊿OMN是等腰直角三角形,∠ONM=90°

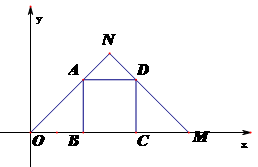
(1) 直接写出N的坐标;

(2) 正方形ABCD是⊿OMN的内接正方形,求正方形边长;

(3) 在（2）的情况下，点P为线段AB上一点,以P为圆心,PB为半径的圆交线段AD于点E.当B,E,N在一条直线上时,求⊙P半径;

(4) 在(3)的情况下,线段CD上取点F,使∠EBF=45°,连结EF,判断直线EF与⊙P是否相切.若是,写出推理过程;若不是,说明理由.

 

Answer 1

(1) N(18,18) (2) 12(3) (4)相切

解析:(1)N(18,18) ---------2分

(2) ∵⊿AOB,⊿CDM是等腰直角三角形

∴OB=AB=BC=CD=CM==12---------3分

∴正方形边长为12

 (3)作NG⊥AD于G点       ∵⊿ABE∽⊿GNE---------1分

∴= =2        ∴AE=4,EG=2---------1分

设⊙P半径为r,则PE=r,AP=AB-PB=12-r

∵Rt⊿APE中,AP²+AE²=PE²    ∴(12-r)²+4²=r²,r=---------2分

(4)延长DC到H,使CH=AE               则⊿ABE≌⊿CBH

∴∠ABE=∠CBH,BE=BH,

∵∠EBF=45°       ∴∠HBF=∠HBC+∠CBF=45°

∴⊿BEF≌⊿BHF---------1分       ∴EF=FH, ---------1分

∵,,

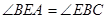∴        ∴PE⊥EF---------1分

直线EF与⊙P相切

 (1)根据等腰直角三角形的性质求解

(2)求得⊿AOB,⊿CDM是等腰直角三角形，则可求得正方形的边长

(3)作NG⊥AD于G点，可得⊿ABE∽⊿GNE，求得AE=4,EG=2，根据勾股定理求得⊙P半径

(4)延长DC到H,使CH=AE，求得⊿ABE≌⊿CBH，⊿BEF≌⊿BHF，利用三角形的角之间的关系，求得，从而得出结论