
����Ŀ��������![]() �У�
��![]() ����
����![]() �͵�
�͵�![]() ���Ǵ�
���Ǵ�![]() ���������
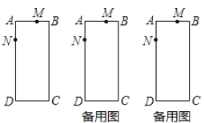
���������![]() ����������εı���˳ʱ���˶�����
����������εı���˳ʱ���˶�����![]() ����������εı�����ʱ���˶������ǵ��ٶȶ���ÿ��1����λ�������ǵ��˶�ʱ����
����������εı�����ʱ���˶������ǵ��ٶȶ���ÿ��1����λ�������ǵ��˶�ʱ����![]() ��
��![]()
��1��![]() ʱ�����߶�
ʱ�����߶�![]() �ij���
�ij���
��2����![]() �˶������У�����
�˶������У�����![]() �����߶�
�����߶�![]() �͵�
�͵�![]() ��������·������ɵķ�յ�ͼ�������
��������·������ɵķ�յ�ͼ�������![]() �����
�����![]() ��
��![]() �ĺ�����ϵʽ����ע��
�ĺ�����ϵʽ����ע��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������һ���У��Ƿ����ij��ʱ��![]() ��ʹ��
��ʹ��![]() �dz�����
�dz�����![]() �����һ�룿�����ڣ����
�����һ�룿�����ڣ����![]() ���������ڣ���˵�����ɣ�
���������ڣ���˵�����ɣ�
��4����![]() ����
����![]() ���˶�ʱ����������
���˶�ʱ����������![]() �����治����ijһʱ��
�����治����ijһʱ��![]() ��ʹ��
��ʹ��![]() ��ֱ���������������ڣ����
��ֱ���������������ڣ����![]() ���������ڣ���˵�����ɣ�
���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3�����ڣ�
����3�����ڣ�![]() ����4�����ڣ�
����4�����ڣ�![]()
��������
��1�����AM��AN�����ù��ɶ�����⼴�ɣ�
��2�����������Σ���0��t��4ʱ����4��t��10ʱ���ֱ���⼴�ɣ�
��3�����ݷ��̽�����⼴�ɣ�
��4���۲�ͼ���֪����MAN����ANM��������ֱ�ǣ�����AMN=90��ʱ������AN2=AM2+MN2���������̼��ɽ�����⣮
�⣺��1����t=3ʱ��AM=3��AN=3��
��Rt��ANM�У��ߡ�MAN=90����
��![]() ��
��
��2����0��t��4ʱ��![]() ��
��
��4��t��10ʱ��
![]() ��
��
��![]()
��3��������![]() ��
��![]() ����
����![]() ��
��![]()
��![]() ��
��
��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
������![]() ��
��![]() �߶Σ���
�߶Σ���![]() ��
��
![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��4������![]() ��
��![]() ���˶�ʱ����MAN����ANM��������ֱ�ǣ�
���˶�ʱ����MAN����ANM��������ֱ�ǣ�
��![]() ʱ����ͼ����M��MG��AN��
ʱ����ͼ����M��MG��AN��
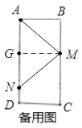
��![]()
������֪��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
������������t��ֵΪ8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
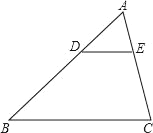
����Ŀ����ͼ����֪��ABC�ס�ADE��AB��30cm��BD��18cm��BC��20cm����BAC��75������ABC��40����
��1����ADE�͡�AED�Ķ�����
��2��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
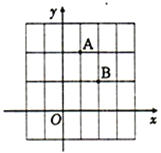
����Ŀ����A��B���������Ϊ1����ͬС������ɵ�����ĸ���ϣ�����ƽ��ֱ������ϵ��ͼ��ʾ.��P��![]() ����ʹ�èOPA��PB�O��ֵ���ĵ㣬Q��
����ʹ�èOPA��PB�O��ֵ���ĵ㣬Q��![]() ����ʹ��QA+QB��ֵ��С�ĵ㣬��OP��OQ=__________.
����ʹ��QA+QB��ֵ��С�ĵ㣬��OP��OQ=__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ACB�У���C=90������O��AB�ϣ���OΪԲ�ģ�OA��Ϊ�뾶��Բ��AC��AB�ֱ��ڵ�D��E������CBD=��A��
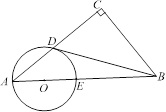
��1���ж�ֱ��BD����O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����AD��AO=8��5��BC=3����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������г���![]() �س���ǰ��
�س���ǰ��![]() �أ�ͬʱ�Ҳ��д�
�أ�ͬʱ�Ҳ��д�![]() �س���ǰ��
�س���ǰ��![]() �أ���ͼ������
�أ���ͼ������![]() ���߶�
���߶�![]() ���ֱ��ʾ�ס���������
���ֱ��ʾ�ס���������![]() �صľ���
�صľ���![]() �� ��
�� ��![]() ������������ʱ��
������������ʱ��![]() ֮��ĺ�����ϵ��
֮��ĺ�����ϵ��
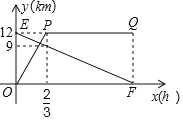
��1�����߶�![]() ��Ӧ��
��Ӧ��![]() ����
����![]() �ĺ�����ϵʽ��ע���Ա���
�ĺ�����ϵʽ��ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ����
����![]() �ĺ�����ϵʽ���ҵ���
�ĺ�����ϵʽ���ҵ���![]() �����õ�ʱ�䣻
�����õ�ʱ�䣻
��3������ Сʱ���ס����������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
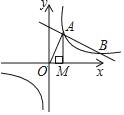
����Ŀ����ͼ��һ�κ���y=��![]() x+
x+![]() ��ͼ���뷴��������y=
��ͼ���뷴��������y=![]() ��k��0����ͼ����A��B���㣬��A����x��Ĵ��ߣ�����ΪM����AOM���Ϊ1��
��k��0����ͼ����A��B���㣬��A����x��Ĵ��ߣ�����ΪM����AOM���Ϊ1��
��1�����������Ľ���ʽ��
��2����y������һ��P��ʹPA+PB��ֵ��С�����������Сֵ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
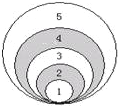
����Ŀ����ͼ��ͬѧ���ڲٳ���һ��Բ����������Ͷ��ɳ������Ϸ��Բ��������5����ͬһ���Ұ뾶��ͬ��Բ��ɣ��������ʵ�飬����ɳ�������������������ʱ������2��4������Ӱ�ڵĸ��ʷֱ���0.36��0.21��������Բ��ֱ����5�ף���1��3��5����������������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���ABC�����������ֱ�Ϊ��A��4��0����B����1��4����C����3��1��
��1����ͼ������A��B��C��ʹ��A��B��C������ABC����x��Գƣ�
��2��д����A��B��C�������ꣻ
��3������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
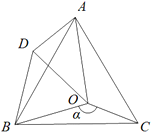
����Ŀ����ͼ����O�ǵȱߡ�ABC��һ�㣬��BOC��![]() ����AOC��100��������BOC�Ƶ�B����ʱ�뷽����ת60���õ���BDA������OD.
����AOC��100��������BOC�Ƶ�B����ʱ�뷽����ת60���õ���BDA������OD.
(1) ��֤����BOD�ǵȱ�������.
(2) ��![]() ��150��ʱ�����жϡ�AOD����״����˵������.
��150��ʱ�����жϡ�AOD����״����˵������.
(3) ����AOD�ǵ��������Σ�����ֱ��д��![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com