
【题目】如图,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上(不与点
上(不与点![]() 重合)的任意一点,连接
重合)的任意一点,连接![]() ,并使
,并使![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,设
,设![]() .
.
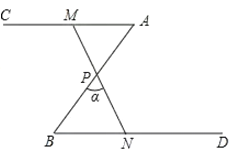
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 的三边垂直平分线的交点在该三角形的内部,直接写出
的三边垂直平分线的交点在该三角形的内部,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)50°;(3)40°<α<90°
【解析】
(1)根据ASA证明:△APM≌△BPN;
(2)由(1)中的全等得:MN=2PN,所以PN=BN,由等边对等角可得结论;
(3)直角三角形的三边垂直平分线的交点是斜边上的中点,钝角三角形的三边垂直平分线的交点在三角形的外部,只有锐角三角形的三边垂直平分线的交点在三角形的内部,所以根据题中的要求可知:△BPN是锐角三角形,由三角形的内角和可得结论.
(1)证明:∵P是AB的中点,
∴PA=PB,
在△APM和△BPN中,
∵ ,
,
∴△APM≌△BPN(ASA);
(2)解:由(1)得:△APM≌△BPN,
∴PM=PN,
∴MN=2PN,
∵MN=2BN,
∴BN=PN,
∴α=∠B=50°;
(3)解:∵![]() 的三边垂直平分线的交点在该三角形的内部,
的三边垂直平分线的交点在该三角形的内部,
∴△BPN是锐角三角形,
∵∠B=50°,
∴40°<∠BPN<90°,即40°<α<90°.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,且
,且![]() 将线段
将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
(1)直接写出![]() __,
__,![]() __ _,点
__ _,点![]() 的坐标为 _;
的坐标为 _;
(2)如图2,作![]() 轴于点
轴于点![]() 点
点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 内部,
内部,![]() 求证:
求证:![]()
(3)如图3,点![]() 是第二象限内的一个动点,若
是第二象限内的一个动点,若![]() 求线段
求线段![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 -![]() ,其中正确的结论个数有_____________________ (填序号)
,其中正确的结论个数有_____________________ (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场准备购进甲.乙两种商品,若购进甲商品80个,乙商品40个,需要800元;若购进甲商品50个,乙商品30个,需要550元.
(1)求商场购进甲.乙两种商品每个需要多少元?
(2)商场准备1000元全部用来购进甲.乙两种商品,计划销售每个甲种商品可获利润4元,销售每个乙种商品可获利润5元,销售这两种玩具的总利润不低于600元,那么商场最多购进乙种商品多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3![]() ,且∠ECF=45°,则CF的长为( )
,且∠ECF=45°,则CF的长为( )

A. 2![]() B. 3
B. 3![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
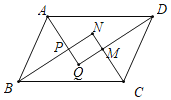
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,且以
,且以![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.

(1)直接写出![]() 点的坐标;
点的坐标;
(2)请用无刻度直尺作直线![]() ,使直线
,使直线![]() 经过点
经过点![]() 且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
(3)已知点![]() 是
是![]() 边上一点,若线段
边上一点,若线段![]() 将菱形
将菱形![]() 的面积分为
的面积分为![]() 两部分,直接写出点
两部分,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
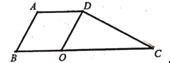
【题目】如图,四边形ABCD中AD∥BC, ∠B=60°,AB=AD=BO=4cm,OC=8cm, 点M从B点出发,按从B→A→D→C的方向,沿四边形BADC的边以1cm/s的速度作匀速运动,运动到点C即停止.若运动的时间为t,△MOD的面积为y,则y关于t的函数图象大约是( )
A. B.
B.
C.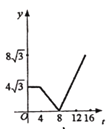 D.
D.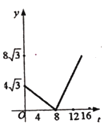
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com