
【题目】如图,是二次函数y=ax2+bx+c的部分图象.

(1)结合图象信息,求此二次函数的表达式;
(2)当y>0时,直接写出x的取值范围: 。
【答案】(1)![]() ; (2)
; (2)![]() 或
或 ![]()
【解析】试题分析:
(1)由图可知,该二次函数的图象的顶点坐标为(1,-4),且过点(-1,0),由此可设其解析式为: ![]() ,再代入点(-1,0)解出a的值即可;
,再代入点(-1,0)解出a的值即可;
(2)根据对称性,由该函数图象与x轴的一个交点坐标为(-1,0)和对称轴为直线x=1可得图象与x轴的另一个交点的坐标为(3,0),结合图象开口向上,即可得到当y>0时,x的取值范围是:x<-1或x>3.
试题解析:
(1)由图可知,该二次函数的图象的顶点坐标为(1,-4),且过点(-1,0),
∴可设其解析式为: ![]() ,
,
将(-1,0)代入![]() ,得:
,得:
![]() ,
,
解得: ![]() ,
,
∴二次函数表达式 ![]() ;
;
(2)由图可知:该函数图象与x轴的一个交点坐标为(-1,0)、对称轴为直线x=1,
∴图象与x轴的另一个交点的坐标为(3,0),
又∵图象开口向上,
∴当y>0时,x的取值范围是:x<-1或x>3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.

(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=2,过点F作MN⊥PE,截取FM=![]() ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中错误的是( )
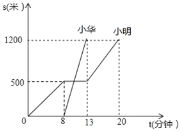
A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米/分
C.小明跑步的平均速度是100米/分
D.小华到学校的时间是7:55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品进价为 70 元,当售价定为每件 100 元时,平均每天可销售 20 件.经调查发现,每件商品每降价 1 元,商场平均每天可多售出 2 件.若商场规定每件商品的利润率不低于 30%,设每件商品降价 x 元.
(1)商场日销售量增加 件,每件商品盈利 元(用含 x 的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,日盈利可达到 750 元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写得数.
1÷0.005= 7.8+3.02= 0.5×0.02= 75%-0.69= 0.023=
![]() +0.025=
+0.025= ![]() ÷0.0625=
÷0.0625= ![]() = 1.2-
= 1.2-![]() ×0= 102×41≈
×0= 102×41≈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
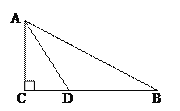
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x | … | -1 | 0 | 2 | 4 | … |
y | … | -5 | 1 | 1 | m | … |
求:(1)这个二次函数的解析式;
(2)这个二次函数图象的顶点坐标及上表中m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com