
【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
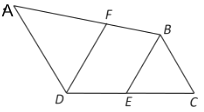
解: 因为DF平分∠CDA,(已知)
所以∠FDC=![]() ∠_________.(____________________)
∠_________.(____________________)
因为∠CDA=120°,(已知)所以∠FDC=______°.
因为DF//BE,(已知)
所以∠FDC=∠_________=60°.(____________________________________)
又因为EC=EB,(已知)
所以△BCE为等边三角形.(________________________________________)
因为△BCE的周长为18cm,(已知) 所以BE=EC=BC=6 cm.
因为点E是DC的中点,(已知) 所以DC=2EC=12 cm .
【答案】ADC;角平分线意义;60;BEC;两直线平行,同位角相等;有一个角是60°的等腰三角形是等边三角形
【解析】
利用角平分线的性质得出∠FDC的度数,再利用平行线的性质得出∠BEC的度数,进而得出△BCE为等边三角形.
∵DF平分∠CDA,(已知)
∴∠FDC=![]() ∠ADC.(角平分线意义)
∠ADC.(角平分线意义)
∵∠CDA=120°,(已知)
∴∠FDC=60°.
∵DF∥BE,(已知)
∴∠FDC=∠BEC=60°.(两直线平行,同位角相等)
又∵EC=EB,(已知)
∴△BCE为等边三角形.(有一个角是60°的等腰三角形是等边三角形)
∵△BCE的周长为18cm,(已知)
∴BE=EC=BC=6cm.
∵点E是DC的中点,(已知)
∴DC=2EC=12cm.


科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为![]() ,
,
①求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
②若当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
(3)将![]() 平移得到抛物线
平移得到抛物线![]() ,使
,使![]() 的顶点
的顶点![]() 落在以原点为圆心半径为
落在以原点为圆心半径为![]() 的圆上,求点
的圆上,求点![]() 与
与![]() 两点间的距离最大时
两点间的距离最大时![]() 的解析式,怎样平移
的解析式,怎样平移![]() 可以得到所求抛物线?
可以得到所求抛物线?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点![]() 的坐标为__________,图2中
的坐标为__________,图2中![]() 的值为__________.
的值为__________.


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
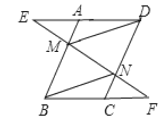
【题目】已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E、F,且AE=CF.
(1) 求证:△AEM≌△CFN.
(2) 求证:四边形BNDM是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,直线![]() 与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
与x轴、y轴分别交于点A、C两点,点B的横坐标为2.

图1 图2
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;
(3)如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com