
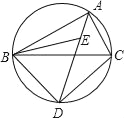
【题目】如图:△ABC是圆的内接三角形,∠BAC与∠ABC的角平分线AE、BE相交于点E,延长AE交圆于点D,连接BD、DC,且∠BCA=60°.
(1)求证:△BED为等边三角形;
(2)若∠ADC=30°,⊙O的半径为2![]() ,求BD长.
,求BD长.
【答案】(1)见解析;(2)4.
【解析】
(1)根据角平分线的定义、三角形内角和定理得到∠DEB=60°,根据圆周角定理得到∠BDA=∠BCA=60°,根据等边三角形的判定定理证明;
(2)根据圆周角定理得到BC是⊙O的直径,根据勾股定理计算即可.
(1)证明:∵∠BAC与∠ABC的角平分线AE、BE相交于点E,
∴∠EAB=![]() ∠CAB,∠EBA=
∠CAB,∠EBA=![]() ∠CBA,
∠CBA,
∴∠AEB=180°﹣(∠EAB+∠EBA)=180°﹣(![]() ∠CAB+
∠CAB+![]() ∠CBA)=180°﹣
∠CBA)=180°﹣![]() (180°﹣∠BCA)=120°,
(180°﹣∠BCA)=120°,
∴∠DEB=60°,
由圆周角定理得,∠BDA=∠BCA=60°,
∴△BED为等边三角形;
(2)∵∠ADC=30°,∠BDA=60°,
∴∠BDC=90°,
∴BC是⊙O的直径,即BC=4![]() ,
,
∵AE平分∠BAC,
∴![]() =
=![]() ,
,
∴BD=DC=4.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.

查看答案和解析>>
科目:初中数学 来源: 题型:
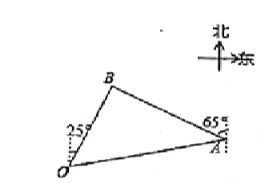
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 与
与![]() 的“广益值”就等于
的“广益值”就等于![]() 的值,可记为
的值,可记为![]()
(1)在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,求
,求![]() ,
,![]() 的值.
的值.
(3)如图3,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m是正实数,关于x的方程2x2﹣mx﹣30=0的两个根为x1、x2,且5x1+3x2=0,在直角坐标系中,抛物线y=mx2+(4+k)x+k与x轴有_____个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
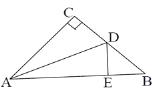
A.4cmB.8cmC.10cmD.14cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com