
 =( );
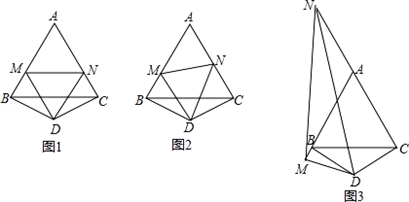
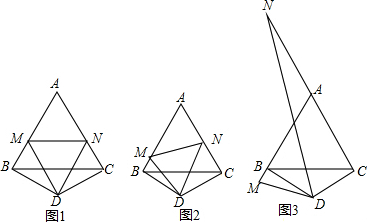
=( );解:(1)如图,BM、NC、MN之间的数量关系BM+NC=MN.此时 . .(2)猜想:结论仍然成立. 证明:如图,延长AC至E,使CE=BM,连接DE. ∵BD=CD,且∠BDC=120°, ∴∠DBC=∠DCB=30°. 又△ABC是等边三角形, ∴∠MBD=∠NCD=90°. 在△MBD与△ECD中:  ∴△MBD≌△ECD(SAS). ∴DM=DE,∠BDM=∠CDE. ∴∠EDN=∠BDC﹣∠MDN=60°. 在△MDN与△EDN中:  , ,∴△MDN≌△EDN(SAS). ∴MN=NE=NC+BM. △AMN的周长Q =AM+AN+MN =AM+AN+(NC+BM) =(AM+BM)+(AN+NC) =AB+AC =2AB. 而等边△ABC的周长L=3AB. ∴  . .(3)如图,当M、N分别在AB、CA的延长线上时,若AN=x, 则Q=2x+ 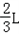 (用x、L表示). (用x、L表示). |
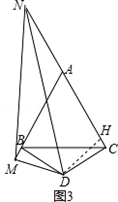  |


科目:初中数学 来源: 题型:
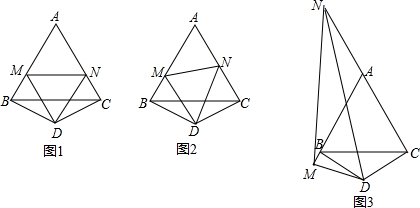
| Q | L |
查看答案和解析>>
科目:初中数学 来源: 题型:
| Q | L |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

 =______;
=______;查看答案和解析>>
科目:初中数学 来源:初三数学圆及旋转题库 第2讲:旋转的应用(解析版) 题型:解答题

 =______;
=______;查看答案和解析>>
科目:初中数学 来源:2009年北京市崇文区中考数学一模试卷(解析版) 题型:解答题
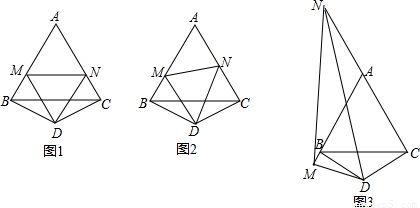
 =______;
=______;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com