
 如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.
如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.分析 (1)根据直线y=kx+3与y轴分别交于B点,以及tan∠OAB=$\frac{3}{4}$,即可得出A点坐标,从而得出一次函数的解析式;
(2)根据△AOC的面积是6,得出三角形的高,即可求出C点的坐标;
(3)利用△BCD与△AOB相似,利用C点不同位置,得出3种不同图形,进而利用相似,得出C点横、纵坐标,进而得出C点坐标.
解答 解:(1)∵直线y=kx+3与y轴分别交于B点,
∴B(0,3),
∵tan∠OAB=$\frac{3}{4}$,
∴OA=4,
∴A(4,0),
∵直线y=kx+3过A(4,0),
∴4k+3=0,
∴k=-$\frac{3}{4}$,
∴直线的解析式为:y=-$\frac{3}{4}$x+3;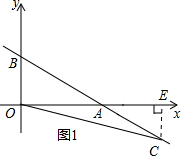
(2)∵A(4,0),
∴AO=4,
∵△AOC的面积是6,
∴△AOC的高为:3,
∴C点的纵坐标为3,
∵直线的解析式为:y=-$\frac{3}{4}$x+3,
∴3=-$\frac{3}{4}$x+3,
x=0,
∴点C运动到B点时,△AOC的面积是6(C是与A、B不重合的动点,所以不符合题意);
如图1,当C点移动到x轴下方时,作CE⊥x轴于点E,
∵△AOC的面积是6,
∴$\frac{1}{2}$EC×AO=6,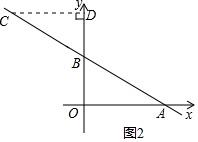
解得:EC=3,
∴C点纵坐标为:-3,
∴C点横坐标为:-3=-$\frac{3}{4}$x+3,
∴x=8,
∴点C点坐标为(8,-3)时,△AOC的面积是6;
(3)①如图2,当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的$\frac{1}{4}$,
∴相似比=$\frac{1}{2}$,∴BD=$\frac{1}{2}$BO=1.5,CD=$\frac{1}{2}$OA=2,
∴C(-2,4.5);
②当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的$\frac{1}{4}$,
∴相似比=$\frac{1}{2}$,∴BD=$\frac{1}{2}$BO=1.5,CD=$\frac{1}{2}$OA=2,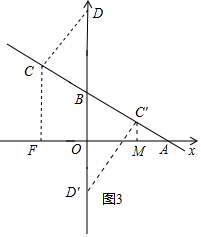
∴C点坐标为:(2,1.5);
③当CD⊥AB时,△BDC∽△BAO,
∵△BCD的面积是△AOB的面积的$\frac{1}{4}$,
∴相似比=$\frac{1}{2}$,
∴BC=1.5,AC=6.5,
过C作CF⊥OA,
则OB∥CF,
∴CF=3.9,FA=5.2,
∴OF=1.2,
∴C(-1.2,3.9);
④当DC⊥AB于点C,△BCD∽△BAO,作CM⊥x轴,
当CB=1.5,BD=2.5,
∴BO∥C′M,
则有OM=1.2,C′M=2.1,
∴C(1.2,2.1).
点评 此题主要考查了待定系数法求一次函数解析式以及相似三角形的判定和性质等知识,根据已知利用图象上点的性质得出点的坐标是解决问题的关键.


科目:初中数学 来源: 题型:解答题
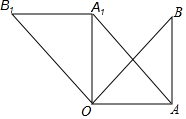 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,连接AA1.
如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,连接AA1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
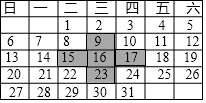 在如图日历中,十字框框出了5个数.
在如图日历中,十字框框出了5个数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com