
【题目】如图,点P是正方形ABCD的对角线BD上的一点,连接PA,PC.
(1)证明:∠PAB=∠PCB;
(2)在BC上截取一点E,连接PE,使得PE=PC,连接AE,判断△PAE的形状,并说明理由.

【答案】(1)证明见解析;(2)△PAE是等腰直角三角形. 理由见解析.
【解析】(1)根据正方形的性质得AB=CB,∠ABD=∠CBD,又知BP=BP,即可证△ABP≌△CBP,于是得到PA=PC,∠PAB=∠PCB;(2)根据PE=PC得到∠PEC=∠PCB,进而求出∠PAB=∠PEC,由E是BC上一点,∠PEB+∠PEC=180°求得∠PAB+∠PEB=180°,进而求出∠APE=90°,再根据PA=PC,PE=PC,求出PA=PE,于是证得△PAE是等腰直角三角形.
解:(1)∵四边形ABCD是正方形,
∴BA=BC,∠ABP=∠CBP ,
又∵BP=BP,
∴△ABP≌△CBP,
∴∠PAB=∠PCB,
(2)△PAE是等腰直角三角形. 理由如下:
∵PE=PC,
∴∠PEC=∠PCB,
由(1)∠PAB=∠PCB,
∴∠PAB=∠PEC ,
∵∠PEC+∠PEB=180°,
∴∠PAB+∠PEB=18,
∵∠PAB+∠ABE+∠PEB+∠APE=360°,
∠ABE=90°,
∴∠APE=90°,
由(1)△ABP≌△CBP得PA=PC,
∵PE=PC,
∴PA= PE,
∴△PAE是等腰直角三角形.
“点睛”本题主要考查正方形的性质和全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握正方形的性质和全等三角形的判定定理,此题难度不大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
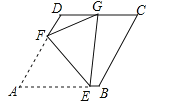
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1光年大约是9050000000000km,用科学记数法表示为( )km.
A.905×1010
B.90.5×1011
C.9.05×1012
D.0.95×1013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com