
【题目】请阅读下列材料,并完成相应的任务.
在数学中,当问题的条件不够时间,常添加辅助线构成新图形,形成新关系,建立已知与未知的桥梁,从而把原问题转化为易于解决的问题.在著名美籍匈牙利数学教波利亚所著的《数学的发现》一书中有这样一个例子:试作一个三角形,使它的三边长分别是各条中线长的三分之一,解决这个问题的步骤如下:

第一步,如图1,己知![]() 的三条中线
的三条中线![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,则有
,则有![]() .
.
下面是该结论的部分证明过程:

证明:如图1,过点![]() 作
作![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
……
第二步,同理可以证明:![]() .
.
第三步,如图2,取BM的中点![]() ,连接
,连接![]() .则
.则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
任务:(1)请在上面第一步中证明过程的基础上完成对结论![]() 的证明;
的证明;
(2)请完成第三步的结论的证明;
(3)请直接写出图2中![]() 与
与![]() 的面积比:
的面积比:![]() _______.
_______.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)证明![]() 即可得到BM=GC,再由
即可得到BM=GC,再由![]() 即可解答;
即可解答;
(2)根据![]() 得出
得出![]() ,再得出
,再得出![]() ,根据中位线的性质得出
,根据中位线的性质得出![]() ,进而得到
,进而得到![]() 即可;
即可;
(3)根据三角形中线将三角形的面积平分即可推出.
(1)解:∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 边上的中线,
边上的中线,
∴![]() .
.
在![]() 和
和![]() 中,
中,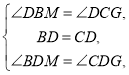
∴![]() (ASA),
(ASA),
∴BM=GC,
∴![]() .
.
(2)证明:∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]()
∵![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
则![]() ,又
,又![]() ,
,
∴![]() .
.
则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
(3)∵Q是BM 的中点,
∴S△BMD=2S△QMD,
∵AM=2MD
∴S△ABM=2S△BMD
∴S△ABD=3S△BMD=6S△QMD,
∵点D是BC中点,
∴S△ABC=2S△ABD=12 S△QMD,
故![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的个数是( )
的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的个数是( )
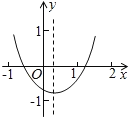
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
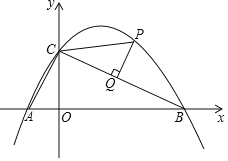
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴相交于点A(-1,0),B(4,0),与
轴相交于点A(-1,0),B(4,0),与![]() 轴相交于点C.
轴相交于点C.
(1)求该函数的表达式;
(2)若点P(2,m)为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC,求线段PQ的长;
(3)在(2)的条件下,点M为该函数图象上一点,且∠MAP=45°,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
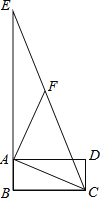
【题目】在探究“尺规三等分角”这个数学命题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是(________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
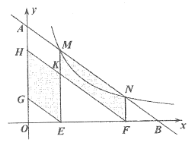
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 和四边形
和四边形![]() 的面积和为12,则
的面积和为12,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com