
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点。

⑴ 填空:AD=CD=_____ .
⑵ 过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为____________.
【答案】10 15.6
【解析】
(1)在△AOD中,由勾股定理可求得AD=10,由AC⊥BD,AO=CO,可知DO是AC的垂直平分线,由线段垂直平分线的性质可知AD=CD=10;
(2)连接DP,根据题意可知S△ADP+S△CDP=S△ADC,由三角形的面积公式可知![]() ADPM+
ADPM+![]() DCPH=
DCPH=![]() ACOD,将AC、OD、AD、DC的长代入化简可知PM+PH为定值9.6,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,PB有最小值6,即可得解.
ACOD,将AC、OD、AD、DC的长代入化简可知PM+PH为定值9.6,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,PB有最小值6,即可得解.
解:(1)∵AC⊥BD于点O,
∴△AOD为直角三角形.
∴AD=![]() =
=![]() =10.
=10.
∵AC⊥BD于点O,AO=CO,
∴AD=CD=10;
(2)如图所示:连接PD,

∵S△ADP+S△CDP=S△ADC,
∴![]() ADPM+
ADPM+![]() DCPH=
DCPH=![]() ACOD,即
ACOD,即![]() ×10×PM+
×10×PM+![]() ×10×PH=
×10×PH=![]() ×16×6,
×16×6,
∴10×(PM+PH)=16×6,
∴PM+PH=9.6,
∴当PB最短时,PM+PH+PB有最小值.
∵由垂线段最短可知:当BP⊥AC时,PB最短,
∴当点P与点O重合时,PM+PH+PB有最小,最小值=9.6+6=15.6.
故答案为:(1)10;(2)15.6.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b+2a=0;②abc>0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )个.
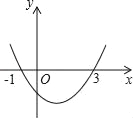
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
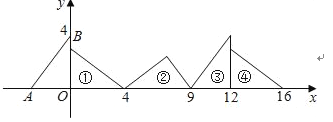
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
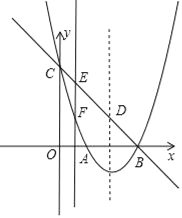
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE。连结DC、BE交于F点。

(1)求证:△DAC≌△BAE;
(2)求证:DC⊥BE;
(3)求证:∠DFA=∠EFA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组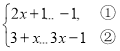
请结合题意填空,完成本题的解答。
(I)解不等式①,得________________
(Ⅱ)解不等式②,得:_____________________
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间t(小时)之间的函数图象是
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块直角三角形木版的一条直角边AB为3m,面积为6![]() ,要把它加工成一个面积最大的正方形桌面,小明打算按图①进行加工,小华准备按图②进行裁料,他们谁的加工方案符合要求?
,要把它加工成一个面积最大的正方形桌面,小明打算按图①进行加工,小华准备按图②进行裁料,他们谁的加工方案符合要求?

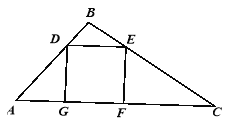
图① 图②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com