【题目】如图，在平行四边形
中，已知
，
，
，点
在
边上，若以
为顶点的三角形是等腰三角形，则
的长是_____．
【答案】2或
或
【解析】
分AB=BP，AB=AP，BP=AP三种情况进行讨论，即可算出BP的长度有三个.
解：根据以
为顶点的三角形是等腰三角形,可分三种情况
①若AB=BP
∵AB=2
∴BP=2
②若AB=AP
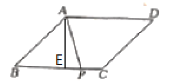
过A点作AE⊥BC交BC于E，
∵AB=AP，AE⊥BC
∴BE=EP
在Rt△ABE中
∵
∴AE=BE
根据勾股定理
AE2+BE2=AB2
即2BE2=4
解得BE=
∴BP=
③若BP=AP，则
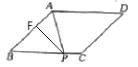
过P点作PF⊥AB
∵AP=BP，PF⊥AB
∴BF=
AB=1
在Rt△BFP中
∵
∴PF=BF=1
根据勾股定理
BP2=BF2+PF2
即BP2=1+1=2，
解得BP=
∵2，，都小于3
故BP=2或BP=或BP=.
科目：初中数学 来源： 题型：
【题目】某市A，B两个蔬菜基地得知四川C，D两个灾民安置点分别急需蔬菜240t和260t的消息后，决定调运蔬菜支援灾区，已知A蔬菜基地有蔬菜200t，B蔬菜基地有蔬菜300t，现将这些蔬菜全部调运C，D两个灾区安置点.从A地运往C，D两处的费用分别为每吨20元和25元，从B地运往C，D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
（1）请填写下表，并求两个蔬菜基地调运蔬菜的运费相等时x的值；
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
（2）设A，B两个蔬菜基地的总运费为w元，求出w与x之间的函数关系式，并求
总运费最小的调运方案；
（3）经过抢修，从B地到C处的路况得到进一步改善，缩短了运输时间，运费每吨减少m元（m＞0），其余线路的运费不变，试讨论总运费最小的调动方案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】骰子是一种特别的数字立方体(见下图)，它符合规则：相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点O为直线AB上一点，过点O作射线OC，使∠AOC：∠BOC=2：1，将一直角的顶点放在点O处，∠MON=90°.
（1）如图1，当∠MON的一边OM与射线OB重合时，则∠NOC=_________；
（2）将∠MON绕点O逆时针运动至图2时，若∠MOC=15°，则∠BOM=______；∠AON=_______.
（3）在上述∠MON从图1运动到图3的位置过程中，当∠MON的边OM所在直线恰好平分∠AOC时，求此时∠NOC是多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示的运算过程中，若开始输入的值为43，我们发现第1次输出的结果为48，第二次输出的结果为24，…，则第2020次输出的结果为_____．
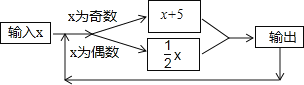
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知两个分别含有30°，45°角的一幅直角三角板．
（1）如图1叠放在一起，若∠CAD=4∠BAD，请计算∠CAE的度数；
（2）如图2叠放在一起，使∠ACE=2∠BCD，请计算∠ACD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
（
，且为常数）．
（
）求证：抛物线与
轴有两个公共点．
（
）若抛物线与轴的一个交点为
，另一个交点为
，与
轴交点为
，直接写出直线
与抛物线对称轴的交点
的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，
的三个顶点的坐标分别为
，
，
，解答下列问题：
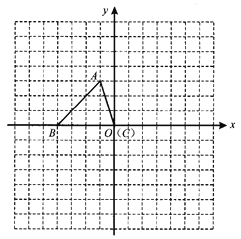
(1)将向上平移1个单位长度，再向右平移5个单位长度后得到的
，画出；
(2)绕原点
逆时针方向旋转
得到
，画出；
(3)如果利用旋转可以得到，请直接写出旋转中心
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
