练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在表达式S=
    		x1-x2+x3-x4
    中，x1、x2、x3、x4是1、2、3、4的一种排列（即：x1、x2、x3、x4取1、2、3、4中的某一个数，且x1、x2、x3、x4互不相同）．则使S为实数的不同排列的种数有
     
    种．
    分析：若不考虑二次根式有意义的条件，因此，共有P44种排列方法，但其中x1+x3=3的共有C24P22种．所以，它们的差即为所求．
    解答：解：∵x1-x2+x3-x4≥0，
    ∴x1+x3≥x2+x4；
    符合条件的排列数是：P44-C42P22=24-8=16（种）
    故答案为：16．
    点评：本题考查了排列与组合的问题．解答此题时，要分清排列与组合的区别．排列与元素的顺序有关，组合与顺序无关．如231与213是两个排列，2+3+1的和与2+1+3的和是一个组合．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

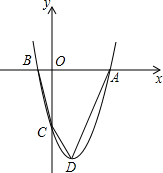    如图，抛物线过点A（x1，0）、B（x2，0）、C（0，-8），x1、x2是方程
    1
    2
    x2-x-4=0的两根，且x1＞x2，点D是此抛物线的顶点．
    （1）求这条抛物线的表达式；
    （2）填空：（1）问题中抛物线先向上平移3个单位，再向右平移2个单位，得到的抛物线是
    y=（x-3）2-6
    y=（x-3）2-6
    ；
    （3）在第一象限内，问题（1）中的抛物线上是否存在点P，使S△ABP=
    1
    5
    S四边形ABCD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•黄石）已知抛物线C1的函数解析式为y=ax2+bx-3a（b＜0），若抛物线C1经过点（0，-3），方程ax2+bx-3a=0的两根为x1，x2，且|x1-x2|=4．
    （1）求抛物线C1的顶点坐标．
    （2）已知实数x＞0，请证明x+
    1
    x
    ≥2，并说明x为何值时才会有x+
    1
    x
    =2．
    （3）若将抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线C2，设A（m，y1），B（n，y2）是C2上的两个不同点，且满足：∠AOB=90°，m＞0，n＜0．请你用含m的表达式表示出△AOB的面积S，并求出S的最小值及S取最小值时一次函数OA的函数解析式．
    （参考公式：在平面直角坐标系中，若P（x1，y1），Q（x2，y2），则P，Q两点间的距离为
    		(x2-x1)2+(y2-y1)2
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知反比例函数表达式为y=
    -4x
    ．
    （1）画出此反比例函数图象并写出此函数图象的一个特征．
    （2）若点（x1，y1），（x2，y2）都在此反比例函数图象上且x1＞x2，比较y1与y2的大小（直接写出结果）
    （3）现有一点A（m，-4）在此反比例函数图象上，另一点B（2，-1），在x轴上找一点P使得△ABP的周长最小，请求出P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2010年湖南省郴州市二中高一奥赛辅导班选拔赛数学试卷（解析版） 题型：填空题

    在表达式S=中，x1、x2、x3、x4是1、2、3、4的一种排列（即：x1、x2、x3、x4取1、2、3、4中的某一个数，且x1、x2、x3、x4互不相同）．则使S为实数的不同排列的种数有     种．

    查看答案和解析>>

    同步练习册答案