已知a2+b2=1,对于满足条件0≤x≤1的一切实数x,不等式a(1-x)(1-x-ax)-bx(b-x-bx)≥0(1)
恒成立.当乘积ab取最小值时,求a,b的值.
解:整理不等式(1)并将a
2+b
2=1代入,得
(1+a+b)x
2-(2a+1)x+a≥0(2)
在不等式(2)中,令x=0,得a≥0;令x=1,得b≥0.
易知1+a+b>0,0<
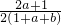
<1,
故二次函数y=(1+a+b)x
2-(2a+1)x+a的图象(抛物线)的开口向上,且顶点的横坐标在0和1之间.
由题设知,不等式(2)对于满足条件0≤x≤1的一切实数x恒成立,
所以它的判别式△=(2a+1)
2-4(1+a+b)a≤0,即ab≥

.
由方程组
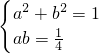
(3)
消去b,得16a
4-16a
2+1=0,所以a
2=
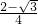
或a
2=

.
又因为a≥0,所以a=

或a=
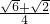
,
于是方程组(3)的解为
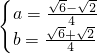
或
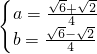
,
所以ab的最小值为

,此时a,b的值有两组,分别为
a=

,b=
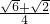
和a=
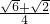
,b=

.
分析:由已知条件a
2+b
2=1,代入已知不等式重新整理,利用特殊值法确定关于a,b的不等式,利用二次函数的增减性,确定判别式的取值范围,进而可以解决.
点评:此题主要考查了二次函数与不等式以及二元二次方程的解法,综合性较强,需耐心思考.

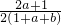 <1,
<1, .
.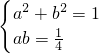 (3)
(3)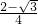 或a2=
或a2= .
. 或a=
或a=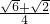 ,
,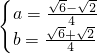 或
或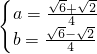 ,
, ,此时a,b的值有两组,分别为
,此时a,b的值有两组,分别为 ,b=
,b=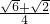 和a=
和a=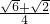 ,b=
,b= .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案