
【题目】若点P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.当三角形的最大角小于120°时,可以证明费马点就是“到三角形的三个顶点的距离之和最小的点“.即PA+PB+PC最小.
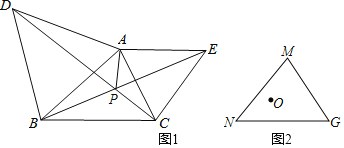
(1)如图1,向△ABC外作等边三角形△ABD,△AEC.连接BE,DC相交于点P,连接AP.
①证明:点P就是△ABC费马点;
②证明:PA+PB+PC=BE=DC;
(2)如图2,在△MNG中,MN=4![]() ,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 .
,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 .
【答案】(1)①证详见解析;②详见解析;(2)![]() .
.
【解析】
(1)①如图1﹣1中,作AM⊥CD于M,AN⊥BE于N设AB交 CD于O.证明△ADC≌△ABE(SAS)即可解决问题.
②在线段PDA上取一点T,使得PA=PT,连接AT.证明△DAT≌△BAP(SAS),推出PD=PA+PB即可解决问题.
(2)以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,可证△GMO≌△DME,可得GO=DE,则MO+NO+GO=NO+OE+DE,即当D、E、O、N四点共线时,MO+NO+GO值最小,最小值为ND的长度,根据勾股定理先求得MF、DF,然后求ND的长度,即可求MO+NO+GO的最小值.
(1)①如图1﹣1中,作AM⊥CD于M,AN⊥BE于N设AB交 CD于O.
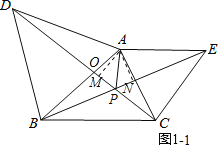
∵△ADB,△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∴∠DAB=∠BAE,
∴△ADC≌△ABE(SAS),
∴CD=BE,S△DAC=S△ABE,∠ADC=∠ABE,
∵AM⊥CD,AN⊥BE,
∴![]() CDAM=
CDAM=![]() BEAN,
BEAN,
∴AM=AN,
∴∠APM=∠APN,
∵∠AOD=∠POB,
∴∠OPB=∠DAO=60°,
∴∠APN=∠APM=60°,
∴∠APC=∠BPC=∠APC=120°,
∴点P是就是△ABC费马点.
②在线段PDA上取一点T,使得PA=PT,连接AT.
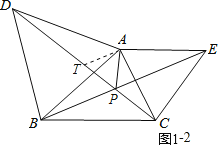
∵∠APT=60°,PT=PA,
∴△APT是等边三角形,
∴∠PAT=60°,AT=AP,
∵∠DAB=∠TAP=60°,
∴∠DAT=∠BAP,∵AD=AB,
∴△DAT≌△BAP(SAS),
∴PB=DT,
∴PD=DT+PT=PA+PB,
∴PA+PB+PC=PD+PC=CD=BE.
(2)如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.
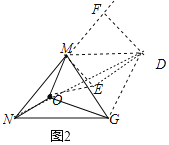
∵△MGD和△OME是等边三角形
∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,
∴∠GMO=∠DME
在△GMO和△DME中,
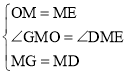 ,
,
∴△GMO≌△DME(
∴OG=DE
∴NO+GO+MO=DE+OE+NO
∴当D、E、O、M四点共线时,NO+GO+MO值最小,
∵∠NMG=75°,∠GMD=60°,
∴∠NMD=135°,
∴∠DMF=45°,
∵MG=3
∴MF=DF=![]() ,
,
∴NF=MN+MF=4![]()
![]() =
=![]() ,
,
∴ND=![]() =
=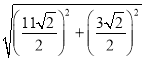 =
=![]() ,
,
∴MO+NO+GO最小值为![]() ,
,
故答案为![]() ,
,


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+1与函数y![]() 的图象交于A(﹣2,a),B两点.
的图象交于A(﹣2,a),B两点.
(1)求a,k的值;
(2)已知点P(0,m),过点P作平行于x轴的直线l,交函数y![]() 的图象于点C(x1,y1),交直线y=﹣x+1的图象于点D(x2,y2),若|x1|>|x2|,结合函数图象,直接写出m的取值范围.
的图象于点C(x1,y1),交直线y=﹣x+1的图象于点D(x2,y2),若|x1|>|x2|,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
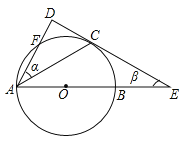
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
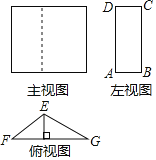
【题目】某几何体的三视图如图所示,已知在△EFG中,FG=18cm,EG=12cm,∠EGF=30°;在矩形ABCD中,AD=16cm.
(1)请根据三视图说明这个几何体的形状.
(2)请你求出AB的长;
(3)求出该几何体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类是必须要落实的国家政策,环卫部门要求垃圾要按![]() 可回收物,
可回收物,![]() 有害垃圾,
有害垃圾,![]() 餐厨垃圾,
餐厨垃圾,![]() 其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).
其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).
(1)直接写出甲投放的垃圾恰好是![]() 类垃圾的概率;
类垃圾的概率;
(2)用树状图求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“ 亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
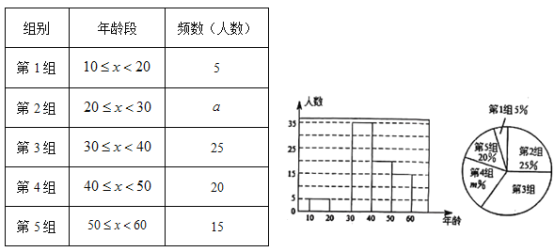
(1)请直接写出![]() _______,
_______,![]() _______,第3组人数在扇形统计图中所对应的圆心角是_______度.
_______,第3组人数在扇形统计图中所对应的圆心角是_______度.
(2)请补全上面的频数分布直方图.
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
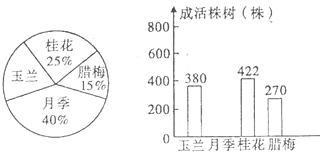
【题目】“不出城郭而获山水之怡,身居闹市而有林泉之致”,合肥市某区不断推进“园林城市”建设,今春种植了四类花苗,园林部门从种植的这批花苗中随机抽取了2000株,将四类花苗的种植株数绘制成扇形统计图,将四类花苗的成活株数绘制成条形统图.经统计这批2000株的花苗总成活率为90%,其中玉兰和月季的成活率较高,根据图表中的信息解答下列问题:
(1)扇形统计图中玉兰所对的圆心角为 ,并补全条形统计图;
(2)该区今年共种植月季8000株,成活了约 株;
(3)园林部门决定明年从这四类花苗中选两类种植,请用列表法或画树状图求恰好选到成活率较高的两类花苗的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com