
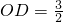 ,试比较S△APC与S△AOC的大小;
,试比较S△APC与S△AOC的大小;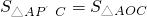 ?若存在,请求出点P′的坐标;若不存在,请说明理由.
?若存在,请求出点P′的坐标;若不存在,请说明理由.
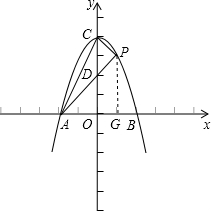 解:(1)由
解:(1)由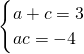
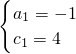 或
或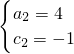 ,
,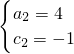 (不合题意,舍去),
(不合题意,舍去), ,
,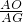 =
=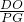 ,
,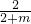 =
=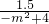 ,
, ,m2=-2(舍去),
,m2=-2(舍去), .
. CD•GO=
CD•GO= ×
× ×
× =
= ,
, AO•DO=
AO•DO= ×2×
×2× =
=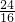 ,
,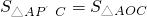 ,
,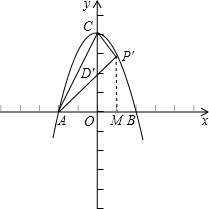
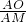 =
=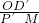 ,即
,即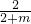 =
=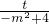 ,
, CD′•OM=
CD′•OM= (4-t)•m,
(4-t)•m, OA•OD′=
OA•OD′= ×2•t=t,
×2•t=t,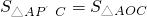 ,
,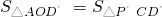 ,
, (4-t)m,即mt+2t=4m ②
(4-t)m,即mt+2t=4m ② -1,m2=-
-1,m2=- -1(不合题意舍去),
-1(不合题意舍去),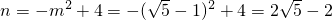 .
. -1,2
-1,2 -2),
-2),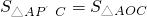 .
. ,再利用已知求出S△PDC,S△AOD的面积,进而得出S△APC与S△AOC的大小关系;
,再利用已知求出S△PDC,S△AOD的面积,进而得出S△APC与S△AOC的大小关系;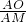 =
=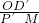 ,以及利用三角形面积关系得出
,以及利用三角形面积关系得出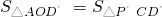 ,进而求出m的值,即可求出点P′的坐标.
,进而求出m的值,即可求出点P′的坐标.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com