
【题目】如图,在Rt△ABC中,∠A=90°,AB=20cm,AC=15cm,在这个直角三角形内有一个内接正方形,正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上.
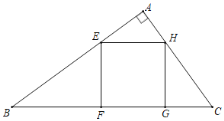
(1)求BC边上的高;
(2)求正方形EFGH的边长.
【答案】(1)12cm;(2)![]()
【解析】
(1)由勾股定理求出BC=25cm,再由三角形面积即可得出答案;
(2)设正方形边长为x,证出△AEH∽△ABC,得出比例式,进而得出答案.
解:(1)作AD⊥BC于D,交EH于O,如图所示:
∵在Rt△ABC中,∠A=90°,AB=20cm,AC=15cm,
∴BC=![]() =25(cm),
=25(cm),
∵![]() BC×AD=
BC×AD=![]() AB×AC,
AB×AC,
∴AD=![]() =
=![]() =12(cm);
=12(cm);
即BC边上的高为12cm;
(2)设正方形EFGH的边长为xcm,
∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=![]() ,
,
即正方形EFGH的边长为![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
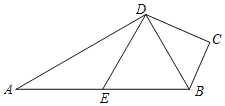
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,AD∥BC,DE与AB交于点F,已知AD=4,DF=2EF,sin∠DAB=![]() ,则线段DE=_____.
,则线段DE=_____.
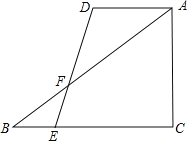
查看答案和解析>>
科目:初中数学 来源: 题型:
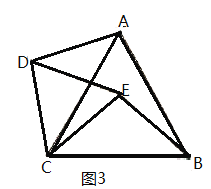
【题目】问题:如图1,等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,显然
,显然![]() .
.

变式:若将图1中的![]() 绕点
绕点![]() 逆时针旋转,使得点
逆时针旋转,使得点![]() 在
在![]() 的内部,其它条件不变(如图2),请你猜想线段
的内部,其它条件不变(如图2),请你猜想线段![]() 与线段
与线段![]() 的关系,并加以证明.
的关系,并加以证明.
拓展:若图2中的![]() 、
、![]() 都为等边三角形,其它条件不变(如图3),则
都为等边三角形,其它条件不变(如图3),则![]() __________,直线
__________,直线![]() 与
与![]() 相交所夹的锐角为__________°.
相交所夹的锐角为__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为DC的中点,AD:AB=![]() :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正确的是( )
;④EFEP=4AOPO.其中正确的是( )
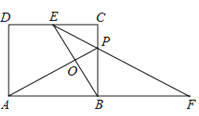
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是:每个大于2的偶数都可以表示为两个素数的和,如16=3+ 13.
(1)若从7, 11, 19, 23中随机抽取1个素数,则抽到的素数是7的概率是_______;
(2)若从7, 11, 19, 23中随机抽取1个素数,再从余下的3个数字中随机抽取1个素数,用面树状图或列表的方法求抽到的两个素数之和大于等于30的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)把表格填写完整;
(2)根据上表填空:
①抛物线与![]() 轴的交点坐标是________和__________;
轴的交点坐标是________和__________;
②在对称轴右侧,![]() 随
随![]() 增大而_______________;
增大而_______________;
③当![]() 时,则
时,则![]() 的取值范围是_________________;
的取值范围是_________________;
(3)请直接写出抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com