
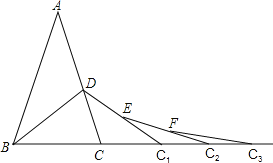
【题目】如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1,连接DC1,使DC=CC1,在CC1延长线上取点C2,在DC1上取点E,使EC1=C1C2,同理FC2=C2C3,若继续如此下去直到Cn,则∠Cn的度数为____.(结果用含![]() 的代数式表示)
的代数式表示)
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 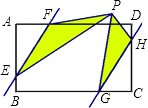
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD内接于⊙O,点E是 ![]() 上一点(不与A、B重合),点F是
上一点(不与A、B重合),点F是 ![]() 上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④若BG=1﹣ ![]() ,则BG,GE,
,则BG,GE, ![]() 围成的面积是
围成的面积是 ![]() +
+ ![]() .
.
其中正确的是(把所有正确结论的序号都填上)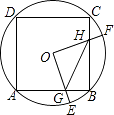
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.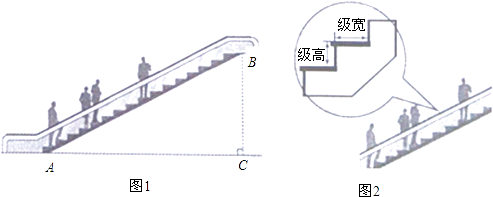
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨以下 | a | 0.80 |
超过17吨但不超过30吨的部分 | b | 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com