
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
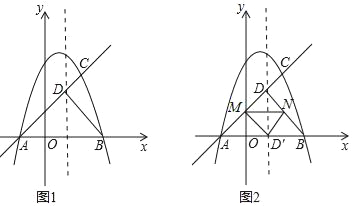
【答案】(1)抛物线的解析式为y=﹣x2+2x+3,点D的坐标为(1,2).(2)四边形DMD′N是正方形,理由见解析,经过![]() s时,点D恰好落在x轴上的D′处.(3)存在,点P的坐标为(1,0)或(2,3).
s时,点D恰好落在x轴上的D′处.(3)存在,点P的坐标为(1,0)或(2,3).
【解析】试题分析:(1)先利用待定系数法求得抛物线和直线的解析式,从而得出对称轴与直线的交点;
(2)由抛物线解析式求得点A、B坐标,结合点D坐标可知△ABD为等腰直角三角形,即∠DAB=∠DBA=45°、∠ADB=90°,由翻折性质得D′M=DM、DN=ND′,从而得出四边形MDND′为菱形,根据∠MDN=90°即可得四边形MDND′为正方形;设DM=DN=t,在Rt△D′NB中D′N=t、BN=2![]() -t、BD′=2,根据勾股定理即可得出t的值;
-t、BD′=2,根据勾股定理即可得出t的值;
(3)由△ABD为等腰直角三角形及△PBD与△ABD相似且不全等,知△PBD是以BD为斜边的等腰直角三角形,结合图形即可得答案.
解:(1)将点A(﹣1,0)、C(2,3)代入y=﹣x2+bx+c,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的对称轴为直线x=1,
设直线AC的函数解析式为y=kx+b,
将A(﹣1,0)、C(2,3)代入y=kx+b,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的函数解析式为y=x+1,
又∵点D是直线AC与抛物线的对称轴的交点,
∴xD=1,yD=1+1=2,
∴点D的坐标为(1,2).
(2)四边形DMD′N是正方形,理由如下:
∵抛物线y=﹣x2+2x+3与x轴交于A、B两点,
∴令y=0,得﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0)、B(3,0),
∴AD=![]() =2
=2![]() ,BD=
,BD=![]() =2
=2![]() ,AB=1+3=4,
,AB=1+3=4,
而AD2+BD2=AB2,
∴△ABD是等腰直角三角形,
∴∠DAB=∠DBA=45°,∠ADB=90°,
由翻折可知:D′M=DM、DN=ND′,
又∵DM=DN,
∴四边形MDND′为菱形,
∵∠MDN=90°,
∴四边形MDND′是正方形;
设DM=DN=t,当点D落在x轴上的点D′处时,
∵四边形MDND′为正方形,
∴∠D′NB=90°,
在Rt△D′NB中,D′N=t,BN=2![]() ﹣t,BD′=2,
﹣t,BD′=2,
∴t2+(2![]() ﹣t)2=22,
﹣t)2=22,
∴t1=t2=![]() ,
,
即:经过![]() s时,点D恰好落在x轴上的D′处.
s时,点D恰好落在x轴上的D′处.
(3)存在,
如图,
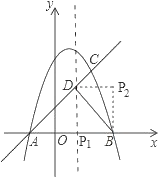
由(2)知△ABD为等腰直角三角形,
∵△PBD与△ABD相似,且不全等,
∴△PBD是以BD为斜边的等腰直角三角形,
∴点P的坐标为(1,0)或(2,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】南宁市青秀区新开发某工程准备招标,指挥部现接到甲、乙两个工程队的投标书,从投标书中得知:乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍;该工程若由甲队先做6天,剩下的工程再由甲、乙两队合作16天可以完成.
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.67万元,乙队每天的施工费用为0.33万元,该工程预算的施工费用为19万元.为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,问:该工程预算的施工费用是否够用?若不够用,需要追加预算多少万元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字2,3,5的三张颜色、质地、大小完全一样的卡片背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并画树状图或列表求出抽取到的两位数恰好是35的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40![]() 厘米,∠CED=60°.
厘米,∠CED=60°.
(1)求垂直支架CD的长度;
(2)求水箱半径OD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
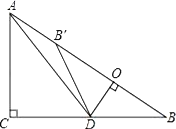
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;

(2)有公共顶点的![]() 条射线可以组成_____个小于平角的角;
条射线可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
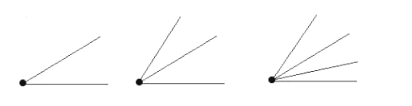
(3)你学过的知识里还有满足类似规律的吗?试看写一个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com