
【题目】如图,等腰直角![]() 中,
中,![]() ,
,![]()
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 上的一个动点,当
上的一个动点,当![]() 点运动时,
点运动时,![]() 的最小值为____
的最小值为____
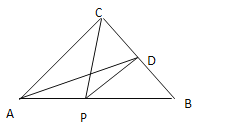
【答案】4
【解析】
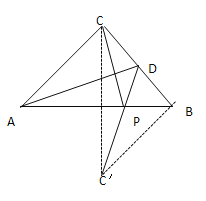
作点C关于AB的对称点C′,连接DC′、BC′,连接DC′交AB于点P,由轴对称的性质易得EC=EC′,则线段DC′的长度即为PC+PD的最小值, 由等腰直角三角形的性质易得∠CBC′=∠CBA+∠C′BA=90![]() ,在Rt△DBC′中,利用勾股定理即可求得线段DC′的长度,问题便可得以解决.
,在Rt△DBC′中,利用勾股定理即可求得线段DC′的长度,问题便可得以解决.
∵![]() ,
,![]()
![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴设CD=x,则AC=2x,
∴x2+(2x)2=42
解得x=![]() ,
,
∴BD=CD=![]() ,BC=AC=
,BC=AC=![]()
如图所示,作点C关于AB的对称点C′,连接DC′、BC′,连接DC′交AB于点E.
∵点C和点C′关于AB对称,
∴PC=PC′,∠CBA=∠C′BA,
∴PC+PD=PC′+PD=DC′,此时PC+PD的长最小.
∵△ABC是等腰直角三角形,AC=BC,
∴∠CBC′=∠CBA+∠C′BA=45![]() +45
+45![]() =90
=90![]() .
.
∴在Rt△DBC′中,由勾股定理得DC′= ![]() =
=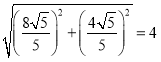 ,
,
∴PC+PD的最小值为4.
故答案为:4.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】问题情景:如图1,在同一平面内,点![]() 和点
和点![]() 分别位于一块直角三角板
分别位于一块直角三角板![]() 的两条直角边
的两条直角边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() 在直线
在直线![]() 的同侧,若点
的同侧,若点![]() 在
在![]() 内部,试问
内部,试问![]() ,
,![]() 与
与![]() 的大小是否满足某种确定的数量关系?
的大小是否满足某种确定的数量关系?
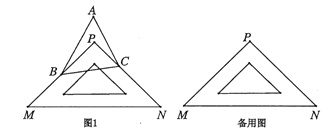
(1)特殊探究:若![]() ,则
,则![]() _________度,
_________度,![]() ________度,
________度,![]() _________度;
_________度;
(2)类比探索:请猜想![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)类比延伸:改变点![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出
外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出![]() ,
,![]() 与
与![]() 满足的数量关系式.
满足的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.
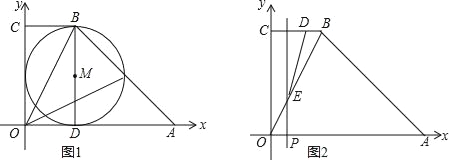
(1)OC的长为 ;
(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ= ;
(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t(秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
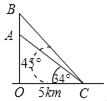
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.
(1)求A,B两点间的距离(结果精确到0.1km).
(2)当运载火箭继续直线上升到D处,雷达站测得其仰角为56°,求此时雷达站C和运载火箭D两点间的距离(结果精确到0.1km).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课外活动小组在做气体压强实验时,获得压强p(Pa)与体积V(cm3)之间有下列对应数据:
p(Pa) | … | 1 | 2 | 3 | 4 | 5 | … |
V(cm3) | … | 6 | 3 | 2 | 1.5 | 1.2 | … |
根据表中提供的信息,回答下列问题:
(1)猜想p与V之间的关系,并求出函数关系式;
(2)当气体的体积是12cm3时,压强是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
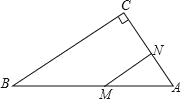
【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在12×10的正方形网格中,△ABC是格点三角形,点B的坐标为(﹣5,1),点C的坐标为(﹣4,5).
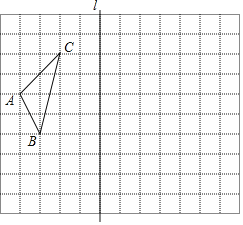
(1)请在方格纸中画出x轴、y轴,并标出原点O;
(2)画出△ABC关于直线l对称的△A1B1C1;
(3)若点P(a,b)在△ABC内,其关于直线l的对称点是P1,则P1的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com