
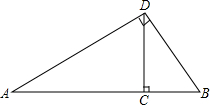
 如图,在Rt△ABD中,∠ADB=90°,CD⊥AB于C,AC=9cm,BC=4cm,求DC及BD的长.
如图,在Rt△ABD中,∠ADB=90°,CD⊥AB于C,AC=9cm,BC=4cm,求DC及BD的长. 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
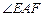 的度数.
的度数. ,
,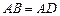 ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且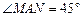 ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转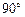 至△ADH位置,连接
至△ADH位置,连接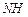 ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由. ,
, ,
,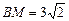 ,求AG,MN的长.
,求AG,MN的长.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北咸宁卷)数学 题型:解答题
(本题满分10分)
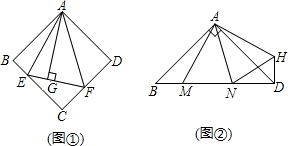
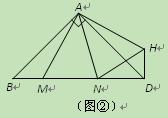
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求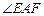 的度数.
的度数.
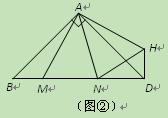
(2)如图②,在Rt△ABD中,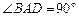 ,
,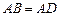 ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且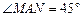 ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转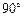 至△ADH位置,连接
至△ADH位置,连接 ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若 ,
,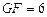 ,
,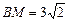 ,求AG,MN的长.
,求AG,MN的长.
查看答案和解析>>
科目:初中数学 来源:2013届安徽滁州八年级第二学期期末数学试卷C(沪科版)(解析版) 题型:解答题
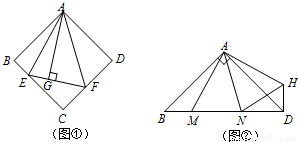
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3,求AG,MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com