
△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲.乙两种剪法,哪种剪法所得的正方形面积大?请说明理由。
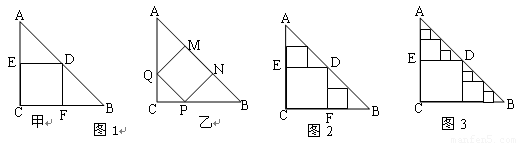
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为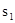 ;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为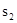 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为
;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为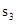 ,继续操作下去……,则第10次剪取时,
,继续操作下去……,则第10次剪取时, ;
;
(3)求第10次剪取后,余下的所有小三角形的面积之和。
(1)甲种剪法所得的正方形面积更大,理由见解析(2)  ,
,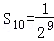 (3)
(3) 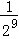
【解析】(1)解法1:如图甲,由题意,得AE=DE=EC,即EC=1,S正方形CFDE=12=1
如图乙,设MN=x,则由题意,得AM=MQ=PN=NB=MN=x,
∴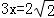 ,
,
解得
∴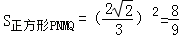
又∵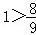
∴甲种剪法所得的正方形面积更大.
说明:图甲可另解为:由题意得点D、E、F分别为AB、AC、BC的中点,S正方形OFDE=1.
解法2:如图甲,由题意得AE=DE=EC,即EC=1,
如图乙,设MN=x,则由题意得AM=MQ=QP=PN=NB=MN=x,
则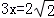 ,
,
解得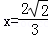 ,
,
又∵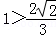 ,即EC>MN.
,即EC>MN.
∴甲种剪法所得的正方形面积更大.
(2) ,
,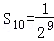 .
.
(3)解法1:探索规律可知: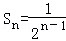
剩余三角形面积和为2﹣(S1+S2+…+S10)=2﹣(1+ +…+
+…+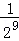 )=
)=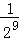
解法2:由题意可知,
第一次剪取后剩余三角形面积和为2﹣S1=1=S1
第二次剪取后剩余三角形面积和为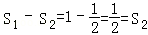 ,
,
第三次剪取后剩余三角形面积和为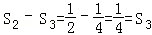 ,
,
…
第十次剪取后剩余三角形面积和为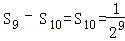 .
.
(1)分别求出甲、乙两种剪法所得的正方形面积,进行比较即可;
(2)按图1中甲种剪法,可知后一个三角形的面积是前一个三角形的面积的 ,依此可知结果;
,依此可知结果;
(3)探索规律可知: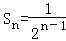 ,依此规律可得第10次剪取后,余下的所有小三角形的面积之和.
,依此规律可得第10次剪取后,余下的所有小三角形的面积之和.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 29 |
| 1 |
| 29 |
| 1 |
| 22011 |
| 1 |
| 22011 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com