
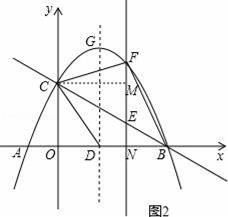
��ͼ��������y=��
 x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
��1���������ߵı���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��3����E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱE������꣮


�����㡿���κ����ۺ��⣮
��ר�⡿���������ۺ��⣻ѹ���⣮
����������1���ɴ���ϵ����������Ԫһ�η�����������m��n��ֵ���ɣ�
��2���ɣ�1���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����P1���Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�P2��P3����CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
��3�������BC�Ľ���ʽ�����E�������Ϊ��a����
 a+2�����Ϳ��Ա�ʾ��F�����꣬���ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
a+2�����Ϳ��Ա�ʾ��F�����꣬���ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
����𡿽⣺��1����������y=��
 x2+mx+n����A����1��0����C��0��2����
x2+mx+n����A����1��0����C��0��2����
��ã�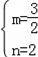
 ��
��
�������ߵĽ���ʽΪ��y=��
 x2+
x2+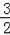
 x+2��
x+2��
��2����y=��
 x2+
x2+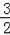
 x+2��
x+2��
��y=��
 ��x��
��x��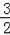
 ��2+
��2+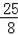
 ��
��
�������ߵĶԳ�����x=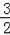
 ��
��
��OD=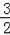
 ��
��
��C��0��2����
��OC=2��
��Rt��OCD�У��ɹ��ɶ�������
CD=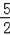
 ��
��
�ߡ�CDP����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3=CD��
��CM��x�Գ�����M��
��MP1=MD=2��
��DP1=4��
��P1��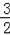
 ��4����P2��
��4����P2��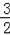
 ��
��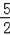
 ����P3��
����P3��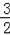
 ����
����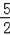
 ����
����
��3����y=0ʱ��0=��
 x2+
x2+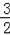
 x+2
x+2
��x1=��1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��
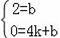
 ��
��
��ã�
 ��
��
��ֱ��BC�Ľ���ʽΪ��y=��
 x+2��
x+2��
��ͼ2������C��CM��EF��M����E��a����
 a+2����F��a����
a+2����F��a����
 a2+
a2+
 a+2����
a+2����
��EF=��
 a2+
a2+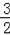
 a+2������
a+2������
 a+2��=��
a+2��=��
 a2+2a��0��a��4����
a2+2a��0��a��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=
 BD•OC+
BD•OC+
 EF•CM+
EF•CM+
 EF•BN��
EF•BN��
=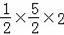
 +
+
 a����
a����
 a2+2a��+
a2+2a��+
 ��4��a������
��4��a������
 a2+2a����
a2+2a����
=��a2+4a+
 ��0��a��4����
��0��a��4����
=����a��2��2+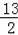

��a=2ʱ��S�ı���CDBF��������=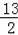
 ��
��
��E��2��1����



�����������⿼���˴���ϵ������һ�κ����Ľ���ʽ�����ã����κ����Ľ���ʽ�����ã����ɶ��������ã����������ε����ʵ����ã��ı��ε���������ã����ʱ��������Ľ���ʽ�ǹؼ���
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�ҵ缯�Ź�˾�����������¼ҵ磬ǰ��Ͷ��200��Ԫ��ÿ����һ̨�����¼ҵ磬���ڻ���Ͷ��0.3��Ԫ����֪ÿ̨�¼ҵ��ۼ�Ϊ0.5��Ԫ������Ͷ��ΪP��Ԫ��������ΪQ��Ԫ��������=�ܲ�ֵ-��Ͷ�ʣ����¼ҵ��ܲ���Ϊx̨��������ɰ��ۼ�ȫ��������
��1������x�Ĵ���ʽ��ʾP��Q��
��2�����ܲ����ﵽ900̨ʱ���ù�˾�ܷ�ӯ����
��3�����ܲ����ﵽ����̨ʱ���ù�˾��ʼӯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪D��E�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬DE��BC��BE��CD�ཻ�ڵ�F�����AE=1��CE=2����ôEF��BF������
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij��������һ������,ƽ��ÿ����۳�100��,ÿ������120Ԫ����������,Ϊ������
����,��������,�������ʵ����ۡ��ݲ���,��ÿ������ÿ����1Ԫ,ÿ��ɶ��۳�2�䡣����������ϵ���������������������⣺
��1����ÿ�����Ͻ���20Ԫʱ����������ÿ�����ۻ�������Ԫ?
��2����Ҫ��ÿ�����ϻ�������80Ԫ������£�Ҫʹÿ���������ϻ���14400Ԫ��
��ÿ��Ӧ���۶���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com