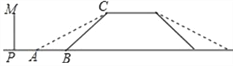
【题目】某地的一座人行天桥如图所示，天桥高为6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1：
．
（1）求新坡面的坡角∠CAB的度数；
（2）原天桥底部正前方8米处（PB的长）的文化墙PM是否需要拆除？请说明理由．
【答案】（1）新坡面的坡角为30°；（2）文化墙PM不需要拆除．
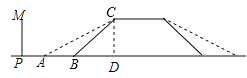
【解析】试题分析：（1）由新坡面的坡度为1：
，由特殊角的三角函数值，即可求得新坡面的坡角；（2）过点C作CD⊥AB于点D，由坡面BC的坡度为1：1，新坡面的坡度为1：．即可求得AD，BD的长，继而求得AB的长，则可求得答案．
试题解析：（1）∵新坡面的坡度为1：，
∴tanα=tan∠CAB=
=
，
∴∠α=30°．
答：新坡面的坡角a为30°；
（2）文化墙PM不需要拆除．
过点C作CD⊥AB于点D，则CD=6，
∵坡面BC的坡度为1：1，新坡面的坡度为1：，
∴BD=CD=6，AD=6，
∴AB=AD﹣BD=6﹣6＜8，
∴文化墙PM不需要拆除．
导学全程练创优训练系列答案科目：初中数学 来源： 题型：
【题目】我们学过角的平分线的概念．类比给出新概念：从一个角的顶点出发，把这个角分成
的两个角的射线，叫做这个角的三分线．显然，一个角的三分线有两条，例如：如图1，若
，则
是
的一条三分线．
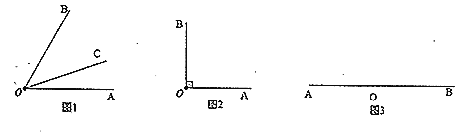
（1）如图1，若
，若
，求
的度数；
（2）如图2，若
，若
是的两条三分线．
①求
的度数；
②现以O为中心，将顺时针旋转
度（
）得到
，当
恰好是的三分线时，则求的值．
（3）如图3，若
，是的一条三分线，
分别是与
的平分线，将
绕点
以每秒
的速度沿顺时针方向旋转一周，在旋转的过程中，若射线
恰好是的三分线，则此时绕点旋转的时间是多少秒？（直接写出答案即可，不必说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果10b＝n，那么称b为n的劳格数，记为b＝d（n）．
（1）根据劳格数的定义，可知：d（10）＝1，d（102）＝2,那么：d（103）＝ ．
（2）劳格数有如下运算性质：若m，n为正数，则d（mn）＝d（m）+d（n）； d（
）＝d（m）﹣d（n）．若d（3）＝0.48，d（2）＝0.3，根据运算性质，填空：d（6）＝ ，则d（
）＝ ，d（
）＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面表格给出了直线
上部分点（x，y）的坐标值．
x | -2 | 0 | 2 | 4 |
y | 3 | 1 | -1 | -3 |
（1）直线与
轴的交点坐标是___________；
（2）直线与两坐标轴围成的三角形的面积等于___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有个填写运算符号的游戏：在“
”中的每个□内，填入
中的某一个（可重复使用），然后计算结果．
（1）计算：
；
（2）若请推算
□内的符号；
（3）在“
”的□内填入符号后，使计算所得数最小，直接写出这个最小数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】全民健身运动已成为一种时尚 ，为了解揭阳市居民健身运动的情况，某健身馆的工作人员开展了一项问卷调查，问卷内容包括五个项目:
A:健身房运动；B:跳广场舞；C:参加暴走团；D:散步；E:不运动.
以下是根据调查结果绘制的统计图表的一部分，
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息，回答下列问题:
接受问卷调查的共有 人，图表中的
，
.
统计图中，
类所对应的扇形的圆心角的度数是 度.
揭阳市环岛路是市民喜爱的运动场所之一，每天都有“暴走团”活动，若某社区约有
人，请你估计一下该社区参加环岛路“暴走团”的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
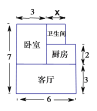
【题目】某人准备购买一套小户型住房，他去某楼盘了解情况得知，该户型单价是
元/
，总面积如图所示（单位：米，卫生间的宽未定，设宽为
米），售房部为他提供了以下两种优惠方案： 方案一：需购买全部总面积，但整套房按原销售总金额的9折出售；
方案二：整套房的单价仍是12000元/，但不需要购买全部面积，其中，只对厨房面积进行了优惠，只算厨房
的面积，其余房间面积不变．
（1）求卫生间的面积；
（2）请分别求出两种方案购买一套该户型商品房的总金额；
（3）当1≤≤2，且为整数时，选哪种方案购买一套该户型商品房的总金额较少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
