
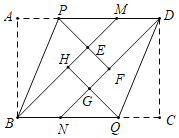
【题目】如图,在矩形纸片ABCD中,BM,DN分别平分∠ABC,∠CDA,沿BP折叠,点A恰好落在BM上的点E处,延长PE交DN于点F沿DQ折叠,点C恰好落在DN上的点G处,延长QG交BM于点H,若四边形EFGH恰好是正方形,且边长为1,则矩形ABCD的面积为____.
【答案】8+6![]() .
.
【解析】
设CQ=x,由角平分可以证明△BHQ,△NQG,△PDF都是等腰直角三角形;根据折叠的性质可知:AP=PE,BE=AB,CD=DG,GQ=CQ;根据边角关系证明△ABP≌△CDQ(ASA)得到AP=CQ;根据以上证明可以得到边的关系:HQ=1+x,HB=1+x,BQ=![]() (1+x),BC=
(1+x),BC=![]() +
+![]() (1+x),CD=NC=x+NQ=x+
(1+x),CD=NC=x+NQ=x+![]() x,DG=x+
x,DG=x+![]() x=1+DF=1+1+x,求出x即可求解;
x=1+DF=1+1+x,求出x即可求解;
设CQ=x,
∵矩形ABCD,BM,DN分别平分∠ABC,∠CDA,
∴∠ABM=∠MBC=∠CDN=∠ADN=45°,
∴△BHQ,△NQG,△PDF都是等腰直角三角形,
∵沿BP折叠,点A恰好落在BM上的点E处,
∴AP=PE,BE=AB,
∵点C恰好落在DN上的点G处,
∴CD=DG,GQ=CQ,
△ABP≌△CDQ(ASA),
∴AP=CQ,
∵正方形EFGH边长为1,
∴HQ=1+x,HB=1+x,
∴BQ=![]() (1+x),BC=
(1+x),BC=![]() +
+![]() (1+x),CD=NC=x+NQ=x+
(1+x),CD=NC=x+NQ=x+![]() x,
x,
∴DG=x+![]() x=1+DF=1+1+x,
x=1+DF=1+1+x,
∴x=![]() ,
,
∴BC=2![]() +2,CD=2+
+2,CD=2+![]() ,
,
∴矩形ABCD的面积=(2![]() +2)(2+
+2)(2+![]() )=8+6
)=8+6![]() ,
,
故答案为8+6![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
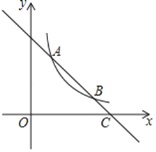
在第一象限的图象交于![]() 和B两点,与
和B两点,与![]() 轴交于点C.
轴交于点C.
(1)求出反比例函数的解析式;
(2)若点P在![]() 轴上,且△APC的面积为5,求点P的坐标.
轴上,且△APC的面积为5,求点P的坐标.
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
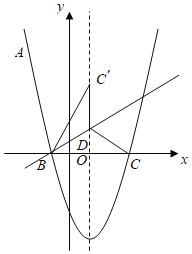
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,
两点,
(1)抛物线的函数表达式;
(2)点![]() 在抛物线的对称轴上,且位于
在抛物线的对称轴上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿沿直线
沿沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)设![]() 是抛物线上位于对称轴右侧的一点,点
是抛物线上位于对称轴右侧的一点,点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一款“雷达式”懒人椅.当懒人椅完全展开时,其侧面示意图如图2所示,金属杆AB、CD在点O处连接,且分别与金属杆EF在点B,D处连接.金属杆CD的OD部分可以伸缩(即OD的长度可变).已知OA=50cm,OB=20cm,OC=30cm.DE=BF=5cm.当把懒人椅完全叠合时,金属杆AB,CD,EF重合在一条直线上(如图3所示),此时点E和点A重合.
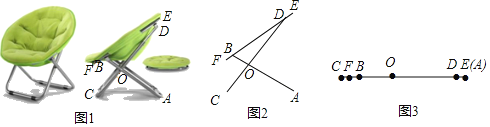
(1)如图2,已知∠BOD=6∠ODB,∠OBF=140°.
①求∠AOC的度数.
②求点A,C之间的距离.
(2)如图3,当懒人椅完全叠合时,求CF与CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一公路相向而行,开往
两地同时出发,沿同一公路相向而行,开往![]() 两地.已知甲车每小时比乙车每小时多走
两地.已知甲车每小时比乙车每小时多走![]() ,且甲车行驶
,且甲车行驶![]() 所用的时间与乙车行驶
所用的时间与乙车行驶![]() 所用的时间相同.
所用的时间相同.
(1)求甲、乙两车的速度各是多少![]() ?
?
(2)实际上,甲车出发后,在途中因车辆故障耽搁了20分钟,但仍比乙车提前1小时到达目的地.求![]() 两地间的路程是多少
两地间的路程是多少![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com