
【题目】如图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为_____.

【答案】114゜
【解析】
如图,设∠B′FE=x,根据折叠的性质得∠BFE=∠B′FE=x,∠AEF=∠A′EF,则∠BFC=x18°,再由第2次折叠得到∠C′FB=∠BFC=x18°,于是利用平角定义可计算出x=66°,接着根据平行线的性质得∠A′EF=180°∠B′FE=114°,所以∠AEF=114°.
解:如图,设∠B′FE=x,
∵纸条沿EF折叠,
∴∠BFE=∠B′FE=x,∠AEF=∠A′EF,
∴∠BFC=∠BFE﹣∠CFE=x﹣18°,
∵纸条沿BF折叠,
∴∠C′FB=∠BFC=x﹣18°,
而∠B′FE+∠BFE+∠C′FE=180°,
∴x+x+x﹣18°=180°,解得x=66°,
∵A′D′∥B′C′,
∴∠A′EF=180°﹣∠B′FE=180°﹣66°=114°,
∴∠AEF=114°.
故答案为:114°.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
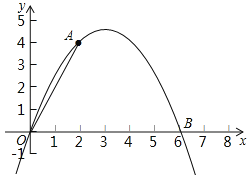
【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图①,在直角三角形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,可知
,可知![]() (不需要证明);
(不需要证明);
(1)探究:如图②,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .证明:
.证明:![]() ;
;
(2)证明:如图③,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 在
在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角。已知
的外角。已知![]() ,
,![]() .求证:
.求证:![]() ;
;
(3)应用:如图④,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,则
的面积为15,则![]() 与
与![]() 的面积之和为________.
的面积之和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) .
.
(2)(﹣2a)3﹣(﹣a)(3a)2.
(3)(x+2)2﹣(x﹣1)(x﹣2).
(4)(a+b)2(a﹣b)2.
(5)(a﹣3)(a+3)(a2+9).
(6)(m﹣2n+3)(m+2n﹣3).
(7) .
.
(8)![]() .
.
(9)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,∠ABG为锐角,AH∥BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为F(F不与A重合),若∠ECF=n°,则∠BAF的度数为_____度.(用n来表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 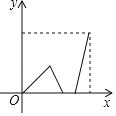
C.  D.
D. 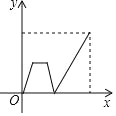
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com