
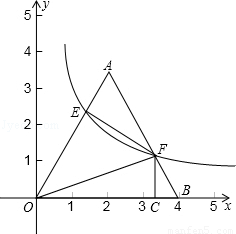
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xoy中,F是AB边上的动点(不与端点A、B重合),过点F的反比例函数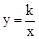 (k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(1)若S△OCF=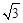 ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与y轴的位置关系,并说明理由;
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.
解:(1)设F(x,y),(x>0,y>0),则OC=x,CF=y,
∴S△OCF=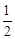 xy=
xy=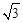 ,即xy=2
,即xy=2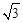 。∴k=2
。∴k=2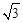 。
。
∴反比例函数解析式为 (x>0)。
(x>0)。
(2)该圆与y轴相离,理由如下:
过点E作EH⊥x轴,垂足为H,过点E作EG⊥y轴,垂足为G,
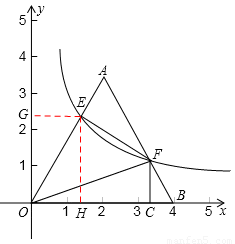
在△AOB中,OA=AB=4,∠AOB=∠ABO=∠A=60°,
设OH=m,则 ,
,
∴EH=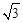 m,OE=2m。∴E坐标为(m,
m,OE=2m。∴E坐标为(m,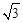 m),
m),
∵E在反比例 图象上,∴
图象上,∴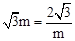 。
。
∴m1=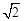 ,m2=-
,m2=-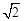 (舍去)。
(舍去)。
∴OE=2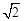 ,EA=4﹣2
,EA=4﹣2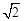 ,EG=
,EG=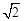 。
。
∵4﹣2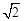 <
<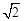 ,∴EA<EG。
,∴EA<EG。
∴以E为圆心,EA垂为半径的圆与y轴相离。
(3)存在。
假设存在点F,使AE⊥FE,
过E点作EH⊥OB于点H,设BF=x.
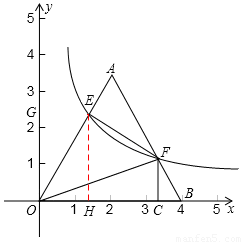
∵△AOB是等边三角形,
∴AB=OA=OB=4,∠AOB=∠ABO=∠A=60°。
∴BC=FB•cos∠FBC=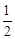 x,FC=FB•sin∠FBC=
x,FC=FB•sin∠FBC=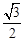 x,
x,
∴AF=4﹣x,OC=OB﹣BC=4﹣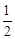 x。
x。
∵AE⊥FE,∴AE=AF•cosA=2﹣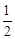 x。
x。
∴OE=OA﹣AE=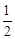 x+2。
x+2。
∴OH=OE•cos∠AOB=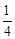 x+1,EH=OE•sin∠AOB=
x+1,EH=OE•sin∠AOB=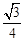 x+
x+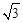 。
。
∴E(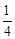 x+1,
x+1,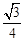 x+
x+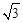 ),F(4﹣
),F(4﹣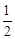 x,
x,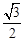 x)。
x)。
∵E、F都在双曲线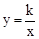 的图象上,
的图象上,
∴(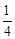 x+1)(
x+1)(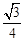 x+
x+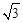 )=(4﹣
)=(4﹣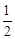 x)•
x)•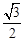 x。解得:x1=4,x2=
x。解得:x1=4,x2=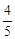 。
。
当BF=4时,AF=0,BF:AF不存在,舍去。
当BF=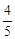 时,AF=
时,AF=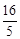 ,BF:AF=1:4
,BF:AF=1:4
【解析】
试题分析:(1)设F(x,y),得到OC=x与CF=y,表示出三角形OCF的面积,求出xy的值,即为k的值,进而确定出反比例解析式。
(2)过E作EH垂直于x轴,EG垂直于y轴,设OH为m,利用等边三角形的性质及锐角三角函数定义表示出EH与OE,进而表示出E的坐标,代入反比例解析式中求出m的值,确定出EG,OE,EH的长,根据EA与EG的大小关系即可对于圆E与y轴的位置关系作出判断。
(3)过E作EH垂直于x轴,设FB=x,利用等边三角形的性质及锐角三角函数定义表示出FC与BC,进而表示出AF与OC,表示出AE与OE的长,得出OE与EH的长,表示出E与F坐标,根据E与F都在反比例图象上,得到横纵坐标乘积相等列出方程,求出方程的解得到x的值,即可求出BF与FA的比值。


科目:初中数学 来源: 题型:
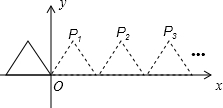 如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是
如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |
3+
| ||
| 2 |
3+
| ||
| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com