
����Ŀ������������12�֣���ͼ���������ϵ�A��B��C��ʾ�����ֱ�Ϊ-2��1��6����A���B֮��ľ����ʾΪAB����B���C֮��ľ����ʾΪBC����A���C֮��ľ����ʾΪAC��
��1����AB=______��BC=______��AC=______��
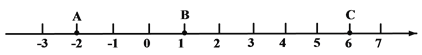
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���������BC��AB��ֵ�Ƿ������˶�ʱ��t�ı仯���ı䣿���仯����˵����������������������ֵ��
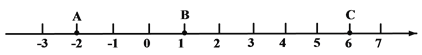
��3���ɵڣ�1��С����Է�����AB+BC=AC������C��ÿ��3����λ���ȵ��ٶ������˶���ͬʱ����A�͵�B�ֱ���ÿ��1����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ������˶��������������˶�ʱ��t�ı仯��AB��BC��AC֮���Ƿ���������ڣ�1����������ϵ����˵��������
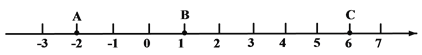
���𰸡���1��AB=3��BC=5��AC=8����2��BC��AB��ֵ��������ʱ��t�ı仯���ı���BC��AB=2 ��
��3����t��1ʱ��AB+BC=AC����1��t��2ʱ��BC+AC=AB����t��2ʱ��AB+AC=BC��
�������������������1�����ݵ�A��B��C�������ϵ�λ�ã�д��AB��BC��AC�ij��ȣ�
��2�����BC��AB��ֵ��Ȼ�����BC-AB��ֵ���жϼ��ɣ�
��3���ֱ��ʾ��AB��BC��AC�ij��ȣ�Ȼ���������۵ó�֮��Ĺ�ϵ��
�����������1����ͼ�ɵã�AB=3��BC=5��AC=8��
��2��BC-AB=��5t-2t+5��-��t+2t+3��=2��
��BC-AB��ֵ��������ʱ��t�ı仯���ı䣻
��3��������ã�AB=t+3��
BC=5-5t��t��1ʱ����BC=5t-5��t��1ʱ����
AC=8-4t��t��2ʱ����AC=4t-8��t��2ʱ����
��t��1ʱ��AB+BC=��t+3��+��5-5t��=8-4t=AC��
��1��t��2ʱ��BC+AC=��5t-5��+��8-4t��=t+3=AB��
��t��2ʱ��AB+AC=��t+3��+��4t-8��=5t-5=BC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һЩ�ֱ������1��2����4��8����16��32�����Ŀ�Ƭ����Щ��Ƭ�ϵ������ǰ�һ���������еģ�С���õ������ڵ����ſ�Ƭ���ҿ�Ƭ�ϵ�����֮��Ϊ96����С���õ������ſ�Ƭ�Ϸֱ����ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������е������߶�����������ε��ǣ� ��
A.2cm��3cm��5cm
B.1cm��6cm��6cm
C.2cm��6cm��9cm
D.5cm��3cm��10cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ⱥ���н���5�·���������������������¼��(��λ����Ԫ)
���� | 14�� | 15�� | 16�� | 17�� | 18�� | 19�� | 20�� |
�������� | 0.20 | 0.17 | 0.23 | 0.21 | 0.23 | 0.18 | 0.25 |
�ɹ�����Ⱥ������һ���µ�������(����)
A. 6.51��Ԫ B. 6.42��Ԫ C. 1.47��Ԫ D. 5.88��Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
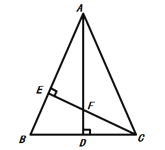
����Ŀ����ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤��
��1����AEF�ա�CEB��
��2��AF=2CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�12��)���κ���y=ax2+bx+c��a��0��������������y=![]() x��ͼ����ͼ��ʾ����ax2+��b��
x��ͼ����ͼ��ʾ����ax2+��b��![]() ��x+c=0��a��0��������֮�ͣ� ��
��x+c=0��a��0��������֮�ͣ� ��
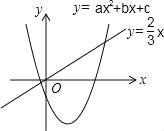
A������0 B������0 C��С��0 D������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
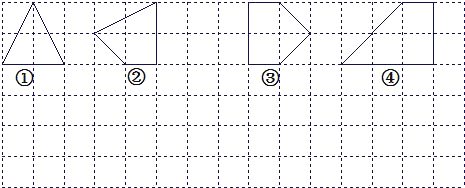
����Ŀ������������11�֣�������һ��̽����Ȥ����Ƥ�˶���������ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ�����С�����εĶ������и�����Ը��Ϊ����Ķ���νи�����Σ��������ε����ΪS���������ϸ��ĸ�����Ϊx��
 ��
��
��1����ͼ�еĸ�����������ڲ���ֻ��һ�������������±�����д��S��x֮��Ĺ�ϵʽ��S=______��

��2��̽��������������ͼ�л����ĸ�������������ڲ���ֻ�������������д�������ĸ�������ε����S���������ϸ��ĸ�����x֮��Ĺ�ϵʽ��S=______��
��3������������������ڲ�����ֻ��n�����ʱ��S��x֮��Ĺ�ϵʽ����S=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��
A.3a��a=3
B.a2+a3=a5
C.����2a��3=��6a3
D.ab2��a=b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ���ȷ����( )
A.2a2-3ab+a=a(2a-3b)
B.2��R-2��r=��(2R-2r)
C.-x2-2x=-x(x-2)
D.5x4+25x2=5x2(x2+5)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com