
【题目】如图,在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 分别在
分别在![]() 轴的正半轴和x轴的正半轴上,
轴的正半轴和x轴的正半轴上,![]() 的面积为
的面积为![]() ,过点
,过点![]() 作直线
作直线![]() 轴.
轴.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是第一象限直线
是第一象限直线![]() 上一动点,连接
上一动点,连接![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 轴于点D,设点
轴于点D,设点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,过点![]() 作直线
作直线![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 与
与![]() 的关系式:
的关系式:![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)由OA=OB,根据面积求出OA的长即可得A点坐标;(2)分0<d<6,d>6,d=6三种情况,当0<d<6时,过C作CH⊥x轴,根据锐角互余的关系可得∠CBH=∠BDO,利用AAS可证明△CBH≌△BDO,进而可得OD=BH,根据OH=AC=d,OH+HB=OB可得d-t=6,同理可得d>6,d=6时,d-t=6;(3)当0<d<6时,由OA=OB,∠AOB=90°,可得∠OAB=∠OBA=45°,在![]() 中,
中,![]() ,可得AE=AD,根据OD=BH,AC=OH,CE=AE+AC可求出CE的长,进而可得OF的长,根据OF=OD可求出t的值,根据(2)所得关系式可求出AC的长进而可得AE的长,即可求出E点坐标,同理可求出d>6时E点坐标,当d=6时,E点不存在.
,可得AE=AD,根据OD=BH,AC=OH,CE=AE+AC可求出CE的长,进而可得OF的长,根据OF=OD可求出t的值,根据(2)所得关系式可求出AC的长进而可得AE的长,即可求出E点坐标,同理可求出d>6时E点坐标,当d=6时,E点不存在.
(1)如图![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∵OA=OB,
∴OA2=36,
∴OA=6
∴点![]() 的坐标为
的坐标为![]()
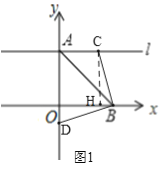
(2)①当0<d<6时,如图1,此时t<0,
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴∠CBH=∠BDO,
∵∠CHB=∠BOD=90°,
∴△CBH≌△BDO,
∴OD=BH,
∵OH=AC=d,OH+HB=OB,
∴d-t=6.
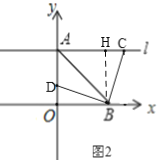
同理,当![]() 时,如图2,可得CH=OD,
时,如图2,可得CH=OD,
∴AC=AH+CH=6+OD,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴d-t=6,
![]() 当
当![]() 时,
时,![]()
∴![]() 与
与![]() 的关系式为d-t=6.
的关系式为d-t=6.
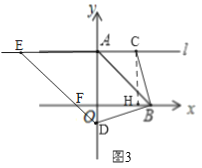
(3)当![]() 时,如图
时,如图![]()
![]()
∴∠ABO=∠BAO=45°,
∵DE//AB,
∴∠EDA=∠BOA=45°,
在![]() 中,
中,![]() ,
,
∴AE=AD,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴t=-2,
∴d-(-2)=6,
∴d=4,即AC=4,
∴EA=CE-AC=12-4=8,
∴点![]() 的坐标为
的坐标为![]()
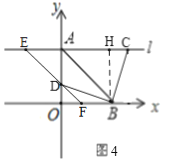
同理,当![]() 时,如图
时,如图![]() ,可得CE=12.OD=OF=
,可得CE=12.OD=OF=![]() =2,
=2,
∴t=2,
∴d-2=6,
∴d=8,即AC=8,
∴AE=12-8=4,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,点
时,点![]() 不存在,
不存在,
综上,点![]() 的坐标为
的坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格纸中,点A、B、C在小正方形的顶点上.
(1)求![]() 的面积;
的面积;
(2)在图中画出与![]() 关于直线1成轴对称的
关于直线1成轴对称的![]() ;
;
(3)在如图所示网格纸中,以![]() 为一边作与
为一边作与![]() 全等的三角形,可以作出多少个三角形与
全等的三角形,可以作出多少个三角形与![]() 全等(不要超出网格纸的范围).
全等(不要超出网格纸的范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() .
.
(1)在图中画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(2)在图中的![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹),并直接写出点
的值最小(保留作图痕迹),并直接写出点![]() 的坐标;
的坐标;
(3)在图中的![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹),并直接写出
的值最小(保留作图痕迹),并直接写出![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2 ![]() ,∠DCF=30°,则EF的长为( )
,∠DCF=30°,则EF的长为( )
A.4
B.6
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款产品,成本价为每件10元.投放市场进行试销,得到如下数据:
售价x(元/件) | … | 30 | 40 | 50 | 60 | … |
日销售量y(件) | … | 50 | 40 | 30 | 20 | … |
(1)若日销售量y(件)是售价x(元/件)的一次函数,求这个一次函数解析式.
(2)设这个工厂试销该产品每天获得的利润为w(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?(每天利润=每天销售总收入﹣每天销售总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2.请用面积法证明:h1+h2=h;

(2)当点M在BC延长线上时,h1、h2、h之间的等量关系式是 ;(直接写出结论不必证明)
(3)如图2在平面直角坐标系中有两条直线l1:y=![]() x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传承优秀传统文化,某校为各班购进![]() 三国演义
三国演义![]() 和
和![]() 水浒传
水浒传![]() 注音读本若干套,其中每套
注音读本若干套,其中每套![]() 三国演义
三国演义![]() 注音读本的价格比每套
注音读本的价格比每套![]() 水浒传
水浒传![]() 注音读本的价格贵60元,用4800元购买
注音读本的价格贵60元,用4800元购买![]() 水浒传
水浒传![]() 注音读本的套数是用3600元购买
注音读本的套数是用3600元购买![]() 三国演义
三国演义![]() 注音读本套数的2倍,求每套
注音读本套数的2倍,求每套![]() 水浒传
水浒传![]() 注音读本的价格.
注音读本的价格.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com