
如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为 .
.
(1)当点P在线段CD上运动时,写出 之间的关系并说出理由;
之间的关系并说出理由;
(2)如果点P在线段CD(或DC)的延长线上运动,探究 之间的关系,并选择其中的一种情况说明理由.
之间的关系,并选择其中的一种情况说明理由.
(1) =
= +
+ ;(2)①当点P在线段DQ(不含端点)时:
;(2)①当点P在线段DQ(不含端点)时: ,②当点P在线段DQ(不含端点)的延长线时:
,②当点P在线段DQ(不含端点)的延长线时: ,③当点P落在线段DC的延长线上时:
,③当点P落在线段DC的延长线上时:
解析试题分析:(1)过P点作PE∥BC,即可得出 之间的关系;
之间的关系;
(2)分三种情况讨论:设直线CD与直线AB相交于点Q
①当点P在线段DQ(不含端点)时: ②当点P在线段DQ(不含端点)的延长线时:
②当点P在线段DQ(不含端点)的延长线时: ③当点P落在线段DC的延长线上时:
③当点P落在线段DC的延长线上时:
试题解析:(1)  =
= +
+
过点P作PE∥AD ∥BC,交AB于点E-
∵PE∥AD
∴ =∠APE
=∠APE
∵PE∥BC
∴ =∠BPE
=∠BPE
∴ =∠APE+∠BPE=
=∠APE+∠BPE= +
+
(2)分三种情况讨论:设直线CD与直线AB相交于点Q
①当点P在线段DQ(不含端点)时:
②当点P在线段DQ(不含端点)的延长线时:
③当点P落在线段DC的延长线上时:

选择一种情况说理正确.
考点:平行线的性质.


科目:初中数学 来源: 题型:解答题
如图,EF∥AD,∠1=∠2,∠BAC=80°,将求∠AGD的过程填写完整.
∵EF//AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3( )
∴AB// ( )
∴∠BAC+ =180°( )
∵∠BAC=80°,
∴∠AGD= 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知)
∴∠2= _________ ( )
又∵∠1=∠2(已知)
∴∠1=∠3( )
∴AB∥ _________ ( )
∴∠BAC+ _________ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
若∠C= ,∠EAC+∠FBC=
,∠EAC+∠FBC=
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则 与
与 有何关系?并说明理由.
有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)
(3)如图③,若 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于 ,
,  ;依此类推,则
;依此类推,则 = (用
= (用 、
、 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知直线 ,直线
,直线 与
与 、
、 分别交于
分别交于 、
、 两点,点
两点,点 是直线
是直线 上的一动点
上的一动点
如图,若动点 在线段
在线段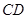 之间运动(不与
之间运动(不与 、
、 两点重合),问在点
两点重合),问在点 的运动过程中是否始终具有
的运动过程中是否始终具有 这一相等关系?试说明理由;
这一相等关系?试说明理由;
如图,当动点 在线段
在线段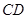 之外且在的上方运动(不与
之外且在的上方运动(不与 、
、 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,那么DG∥BC吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com