
【题目】对于△ABC及其边上的点P,给出如下定义:如果点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 都在△ABC的边上,且
都在△ABC的边上,且![]() ,那么称点
,那么称点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距点,线段
为△ABC关于点P的等距点,线段![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距线段.
为△ABC关于点P的等距线段.
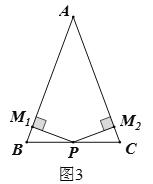
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.

①点B,C △ABC关于点P的等距点,线段PA,PB △ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点![]() ,
,![]() 分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段
分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段![]() ,
,![]() ;
;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
(3)如图2,在Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点![]() .若
.若![]() ,直接写出
,直接写出![]() 长的取值范围.(用含
长的取值范围.(用含![]() 的式子表示)
的式子表示)

【答案】(1)①是,不是;②见解析;(2)DC=1或2;(3)![]() .
.
【解析】
(1)①根据阅读材料中△ABC关于点P的等距点和△ABC关于点P的等距线段的定义判断即可;
②根据题意,点P在∠BAC的平分线上,要使相应的等距线段最短,只要过点P作AB、AC的垂线段即可;
(2)显然点D不可能在AB边上,分点D在等边△ABC的边AC、BC上,画出图形,然后根据等距点的概念和等边三角形的判定与性质求解即可;
(3)先求出△ABC关于点P的等距点恰好有3个,且其中一个是点![]() 时的PC的长,进而可得答案.
时的PC的长,进而可得答案.
解:(1)①∵点P是BC的中点,∴PB=PC,∴点B、C是△ABC关于点P的等距点;
∵PA≠PB,∴线段PA,PB不是△ABC关于点P的等距线段;
故答案为:是,不是;
②线段![]() ,
,![]() 如图3所示:
如图3所示:
(2)显然,点D不可能在AB边上,若点D在AC边上,如图4所示,
∵△ABC是等边三角形,∴∠C=60°,
∵点C,D是△ABC关于点P的等距点,∴PC=PD,
∴△PCD是等边三角形,∴CD=PC=1;
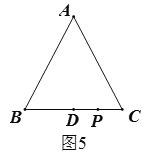
若点D在BC边上,如图5所示,∵点C,D是△ABC关于点P的等距点,∴PC=PD=1,∴CD=2;
∴DC=1或2;
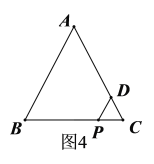
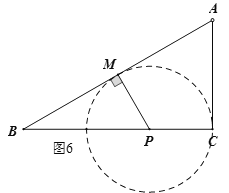
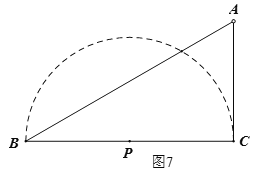
(3)当PM⊥AB且PM=PC时,如图6,此时△ABC关于点P的等距点恰好有3个,且其中一个是点![]() ,
,
∵∠B=30°,∴BP=2PM,∴BC=3PC=a,∴![]() ;
;
当点P为BC的中点时,如图7所示,此时△ABC关于点P的等距点恰好有3个,且其中一个是点![]() ,∴
,∴![]() ;
;
∴△ABC关于点P的等距点恰好有四个,且其中一个是点![]() 时,PC长的取值范围是:
时,PC长的取值范围是:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )

A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
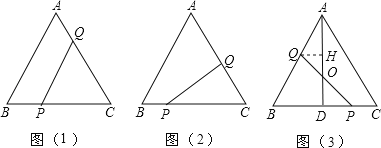
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②a+b+c<0;③b2>4ac;④3a+c<0.其中正确的是( )

A. ①④ B. ②③④ C. ①②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON![]() 60°,点A是OM边上一点,点B,C是ON边上两点,且AB
60°,点A是OM边上一点,点B,C是ON边上两点,且AB![]() AC,作点B关于OM的对称点点D,连接AD,CD,OD.
AC,作点B关于OM的对称点点D,连接AD,CD,OD.
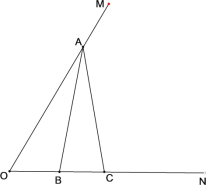

(1)依题意补全图形;
(2)猜想∠DAC![]() °,并证明;
°,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定在网格内的某点进行一定条件操作到达目标点:H代表所有的水平移动,H1代表向右水平移动1个单位长度,H-1代表向左平移1个单位长度;S代表上下移动,S1代表向上移动1个单位长度,S-1代表向下移动1个单位长度,![]() 表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;
表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;![]() 表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
(1)如图,在网格中标出![]() 移动后所到达的目标点
移动后所到达的目标点![]() ;
;

(2)如图,在网格中的点B到达目标点A,写出点B的移动方法________________;

(3)如图,在网格内有格点线段AC,现需要由点A出发,到达目标点D,使得A、C、D三点构成的格点三角形是等腰直角三角形,在图中标出所有符合条件的点D的位置并写出点A的移动方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“在一个三角形中,至少有一个内角小于或等于![]() ”的过程如下:
”的过程如下:
已知: ![]() ;
;
求证: ![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
证明:假设![]() 中没有一个内角小于或等于
中没有一个内角小于或等于![]() ,即
,即![]() ,则
,则
![]() ,
,
这与“__________” 这个定理相矛盾,
所以![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
在证明过程中,横线上应填入的句子是( )
A.三角形内角和等于![]() B.三角形的一个外角等于与它不相邻的两个内角的和
B.三角形的一个外角等于与它不相邻的两个内角的和
C.等边三角形的各角都相等,并且每个角都等于![]() D.等式的性质
D.等式的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
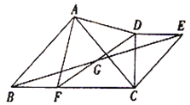
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表.设分配给甲店A型产品![]() 件,这家公司卖出这100件产品的总利润为W(元).
件,这家公司卖出这100件产品的总利润为W(元).

(1)求W关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案?
(3)实际销售过程中,公司发现这批产品尤其是A型产品很畅销,便决定对甲店的最后21件A型产品每件提价![]() 元销售(
元销售(![]() 为正整数).两店全部销售完毕后结果的总利润为18000元,求
为正整数).两店全部销售完毕后结果的总利润为18000元,求![]() 值.并写出公司这100件产品对甲乙两店是如何分配的?
值.并写出公司这100件产品对甲乙两店是如何分配的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com