
ЁОЬтФПЁПЯТУцИјГіСљИіКЏЪ§НтЮіЪНЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
аЁУїИљОнбЇЯАЖўДЮКЏЪ§ЕФОбщЃЌЗжЮіСЫЩЯУцетаЉКЏЪ§НтЮіЪНЕФЬиЕуЃЌбаОПСЫЫќУЧЕФЭМЯѓКЭаджЪЁЃЯТУцЪЧаЁУїЕФЗжЮіКЭбаОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЙлВьЩЯУцетаЉКЏЪ§НтЮіЪНЃЌЫќУЧЖМОпгаЙВЭЌЕФЬиЕуЃЌПЩвдБэЪОЮЊаЮШч![]() _______ЃЌЦфжаxЮЊздБфСПЃЛ
_______ЃЌЦфжаxЮЊздБфСПЃЛ
ЃЈ2ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЛГіСЫКЏЪ§
жаЃЌЛГіСЫКЏЪ§![]() ЕФВПЗжЭМЯѓЃЌгУУшЕуЗЈНЋетИіКЏЪ§ЕФЭМЯѓВЙГфЭъећЃЛ
ЕФВПЗжЭМЯѓЃЌгУУшЕуЗЈНЋетИіКЏЪ§ЕФЭМЯѓВЙГфЭъећЃЛ
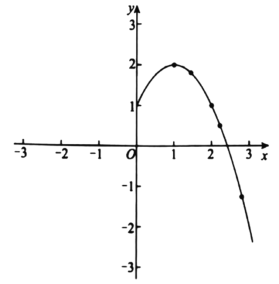
ЃЈ3ЃЉЖдгкЩЯУцетаЉКЏЪ§ЃЌЯТСаЫФИіНсТлЃК
ЂйКЏЪ§ЭМЯѓЙигкyжсЖдГЦ
ЂкгааЉКЏЪ§МШгазюДѓжЕЃЌЭЌЪБвВгазюаЁжЕ
ЂлДцдкФГИіКЏЪ§ЃЌЕБ![]() ЃЈmЮЊе§Ъ§ЃЉЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЕБ
ЃЈmЮЊе§Ъ§ЃЉЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁ
ЂмКЏЪ§ЭМЯѓгыxжсЙЋЙВЕуЕФИіЪ§жЛПЩФмЪЧ0ИіЛђ2ИіЛђ4Иі
Ыљгае§ШЗНсТлЕФађКХЪЧ________ЃЛ
ЃЈ4ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКШєЙигкxЕФЗНГЬ![]() гавЛИіЪЕЪ§ИљЮЊ3ЃЌдђИУЗНГЬЦфЫќЕФЪЕЪ§ИљЮЊ_______ЃЎ
гавЛИіЪЕЪ§ИљЮЊ3ЃЌдђИУЗНГЬЦфЫќЕФЪЕЪ§ИљЮЊ_______ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈaЁй0ЃЉЃЛЃЈ2ЃЉЭМЯѓМћЯъНтЃЛЃЈ3ЃЉЂйЂлЃЛЃЈ4ЃЉ
ЃЈaЁй0ЃЉЃЛЃЈ2ЃЉЭМЯѓМћЯъНтЃЛЃЈ3ЃЉЂйЂлЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЙлВьСљИіЖўДЮКЏЪ§НтЮіЪНЕФЬиЕуЃЌПЩжЊЃКЫќУЧЖМОпгаЙВЭЌЕФЬиЕуЃКвЛДЮЯюЕФxКЌгаОјЖджЕЃЌМДПЩЃЛ
ЃЈ2ЃЉИљОнЧѓОјЖджЕЗЈдђЃЌЕБx<0ЪБЃЌ![]() ЃЌдйгУУшЕуЗЈЃЌЛГіЭМЯѓЃЌМДПЩ.
ЃЌдйгУУшЕуЗЈЃЌЛГіЭМЯѓЃЌМДПЩ.
ЃЈ3ЃЉНсКЯСљИіЖўДЮКЏЪ§ЕФЖюЭМаЮКЭаджЪЃЌж№вЛХаЖЯЃЌМДПЩЃЛ
ЃЈ4ЃЉЯШЧѓГіkЕФжЕЃЌдйСю![]() ЃЌ
ЃЌ ![]() ЃЌдкЭЌвЛзјБъЯЕжаЃЌЛГіЭМЯѓЃЌИљОнСНИіКЏЪ§ЭМЯѓЕФНЛЕузјБъЃЌМДПЩЕУЕНД№АИ.
ЃЌдкЭЌвЛзјБъЯЕжаЃЌЛГіЭМЯѓЃЌИљОнСНИіКЏЪ§ЭМЯѓЕФНЛЕузјБъЃЌМДПЩЕУЕНД№АИ.
ЃЈ1ЃЉЙлВьСљИіЖўДЮКЏЪ§НтЮіЪНЕФЬиЕуЃЌПЩжЊЃКЫќУЧЖМОпгаЙВЭЌЕФЬиЕуЃКвЛДЮЯюЕФxКЌгаОјЖджЕЃЌМДЃК![]() ЃЈaЁй0ЃЉЃЌ
ЃЈaЁй0ЃЉЃЌ
ЙЪД№АИЪЧЃК![]() ЃЈaЁй0ЃЉЃЛ
ЃЈaЁй0ЃЉЃЛ
ЃЈ2ЃЉЕБx<0ЪБЃЌ![]() ЃЌИљОнУшЕуЗЈЃЌШчЭМЫљЪОЃК
ЃЌИљОнУшЕуЗЈЃЌШчЭМЫљЪОЃК
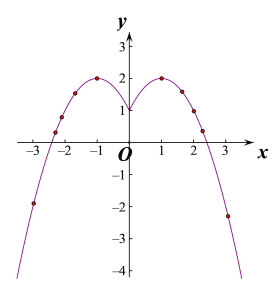
ЃЈ3ЃЉЁп![]() ЃЌ
ЃЌ![]() ЃЌЙигкyжсЖдГЦЃЌ
ЃЌЙигкyжсЖдГЦЃЌ
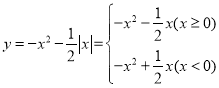 ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
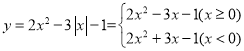 ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
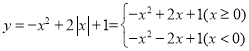 ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
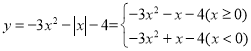 ЃЌЭМЯѓЙигкyжсЖдГЦЃЎ
ЃЌЭМЯѓЙигкyжсЖдГЦЃЎ
ЁрЂйе§ШЗЃЛ
Ёп![]() ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
![]() ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
![]() ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
![]() ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
ЃЌгазюаЁжЕЃЌУЛгазюДѓжЕЃЌ
![]() ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
![]() ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
ЃЌгазюДѓжЕЃЌУЛгазюаЁжЕЃЌ
ЁрЂкДэЮѓЃЛ
Ёп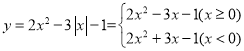 ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
ЃЌЭМЯѓЙигкyжсЖдГЦЃЌ
ЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЕБ
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЂле§ШЗЃЛ
Ёп![]() ЕФЭМЯѓгыxжсга1ИіЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсга1ИіЙЋЙВЕуЃЌ
![]() ЕФЭМЯѓгыxжсУЛгаЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсУЛгаЙЋЙВЕуЃЌ
![]() ЕФЭМЯѓгыxжсга1ИіЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсга1ИіЙЋЙВЕуЃЌ
![]() ЕФЭМЯѓгыxжсга2ИіЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсга2ИіЙЋЙВЕуЃЌ
![]() ЕФЭМЯѓгыxжсга2ИіЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсга2ИіЙЋЙВЕуЃЌ
![]() ЕФЭМЯѓгыxжсУЛгаЙЋЙВЕуЃЌ
ЕФЭМЯѓгыxжсУЛгаЙЋЙВЕуЃЌ
ЁрЂмДэЮѓЃЌ
ЙЪД№АИЪЧЃКЂйЂлЃЛ
ЃЈ4ЃЉЁпЙигкxЕФЗНГЬ![]() гавЛИіЪЕЪ§ИљЮЊ3ЃЌ
гавЛИіЪЕЪ§ИљЮЊ3ЃЌ
Ёр![]() ЃЌНтЕУЃКk=1ЃЌ
ЃЌНтЕУЃКk=1ЃЌ
Сю![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
КЏЪ§ЭМЯѓШчЭМЫљЪОЃК
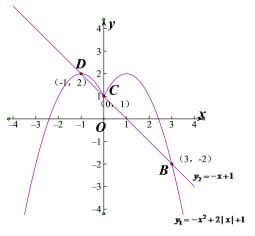
ЁрЙигкxЕФЗНГЬ![]() ЕФЦфЫћСНИіЪЕЪ§ИљЮЊЃК
ЕФЦфЫћСНИіЪЕЪ§ИљЮЊЃК![]() ЃЌ
ЃЌ
ЙЪД№АИЪЧЃК![]()


 ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИ
ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
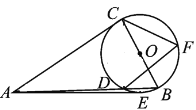
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌвдBCЮЊжБОЖЕФЁбOНЛABгкЕуDЃЌEЁЂFЪЧЁбOЩЯЕФСНЕуЃЌСЌНсAEЁЂCFЁЂDFЃЌТњзуEAЃНCA.
(1)ЧѓжЄЃКAEЪЧЁбOЕФЧаЯпЃЛ
(2)ШєЁбOЕФАыОЖЪЧ3ЃЌtanЁЯCFDЃН![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЁЯC=90ЁуЃЌOЪЧаББпABЩЯвЛЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖЕФдВгыABНЛгкЕуEЃЌгыBCНЛгкЕуFЃЌгыACЯрЧагкЕуDЃЌСЌНгDFЁЂBDЃЌЧвBDЦНЗжЁЯODFЃЎ
жаЃЌЁЯC=90ЁуЃЌOЪЧаББпABЩЯвЛЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖЕФдВгыABНЛгкЕуEЃЌгыBCНЛгкЕуFЃЌгыACЯрЧагкЕуDЃЌСЌНгDFЁЂBDЃЌЧвBDЦНЗжЁЯODFЃЎ
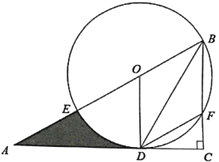
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓвѕгАВПЗжЕФУцЛ§(НсЙћБЃСє
ЃЌЧѓвѕгАВПЗжЕФУцЛ§(НсЙћБЃСє![]() )ЃЎ
)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
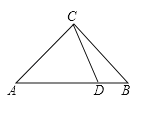
ЁОЬтФПЁПвбжЊЃКдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌDЪЧЯпЖЮABЩЯвЛЕуЃЌСЌНсCDЃЌНЋЯпЖЮCDШЦЕуCФцЪБеыа§зЊ90ЁуЕУЕНЯпЖЮCEЃЌСЌНсDEЃЌBEЃЎ
ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉШєЁЯACD=ІСЃЌгУКЌІСЕФДњЪ§ЪНБэЪОЁЯDEBЃЛ
ЃЈ3ЃЉШєЁїACDЕФЭтаФдкШ§НЧаЮЕФФкВПЃЌЧыжБНгаДГіІСЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉаДГіИУЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсМАЖЅЕузјБъЃЌдйУшЕуЛЭМЃЛ
ЃЈ2ЃЉРћгУЭМЯѓЛиД№ЃКЕБxШЁЪВУДжЕЪБЃЌ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФЖЅЕуAЃЌBЗжБ№дкyжсЁЂxжсЩЯЃЌOAЃН2ЃЌOBЃН1ЃЌаББпACЁЮxжсЃЎШєЗДБШР§КЏЪ§y![]() ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ACЕФжаЕуDЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§ACЕФжаЕуDЃЌдђkЕФжЕЮЊЃЈ ЃЉ

A.4B.5C.6D.8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
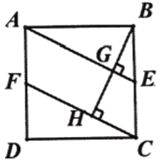
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯABCЃН30ЁуЃЌЁїCDEЪЧЕШБпШ§НЧаЮЃЌЕуDдкБпABЩЯЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуEдкБпBCЩЯЪБЃЌЧѓжЄDEЃНEBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкЁїABCФкВПЪБЃЌВТЯыEDКЭEBЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
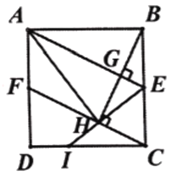
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуEдкЁїABCЭтВПЪБЃЌEHЁЭABгкЕуHЃЌЙ§ЕуEзїGEЁЮABЃЌНЛЯпЖЮACЕФбгГЄЯпгкЕуGЃЌAGЃН5CGЃЌBHЃН3ЃЎЧѓCGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌе§ЗНаЮ![]() жаЃЌ Еу
жаЃЌ Еу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ДЙжБ
ДЙжБ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНг![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гкЕуIЃЌ
гкЕуIЃЌ
ЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
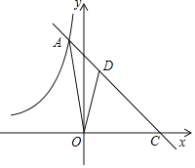
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌКЏЪ§yЃНЉx+5ЕФЭМЯѓгыКЏЪ§yЃН![]() ЃЈkЃМ0ЃЉЕФЭМЯѓЯрНЛгкЕуAЃЌВЂгыxжсНЛгкЕуCЃЌSЁїAOCЃН15ЃЎЕуDЪЧЯпЖЮACЩЯвЛЕуЃЌCDЃКACЃН2ЃК3ЃЎ
ЃЈkЃМ0ЃЉЕФЭМЯѓЯрНЛгкЕуAЃЌВЂгыxжсНЛгкЕуCЃЌSЁїAOCЃН15ЃЎЕуDЪЧЯпЖЮACЩЯвЛЕуЃЌCDЃКACЃН2ЃК3ЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉИљОнЭМЯѓЃЌжБНгаДГіЕБxЃМ0ЪБВЛЕШЪН![]() ЃОЉx+5ЕФНтМЏЃЛ
ЃОЉx+5ЕФНтМЏЃЛ
ЃЈ3ЃЉЧѓЁїAODЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com