
 ̉ÑÖªÁ½̀ơÖ±Ïßl1¡¢l2·Ö±đ¾¹ưµăA£¨-1£¬0£©¡¢µăB£¨3£¬0£©²¢Ç̉µ±Á½̀ơÖ±ÏßͬʱÏཻÓÚyÖáµÄ¸º°ëÖáÉϵĵăCʱ£¬Ç¡ºĂÓĐl1¡Íl2£¬¾¹ưµăA¡¢B¡¢CµÄÅ×ÎïÏߵĶԳÆÖáÓëÖ±Ïßl1½»ÓÚµăK£¬ÓëÖ±Ïßl2½»ÓÚµăE£¬ÔÚxÖá½»ÓÚµăF£¬DÊÇÅ×ÎïÏߵĶ¥µă£¬ÈçͼËùʾ£®
̉ÑÖªÁ½̀ơÖ±Ïßl1¡¢l2·Ö±đ¾¹ưµăA£¨-1£¬0£©¡¢µăB£¨3£¬0£©²¢Ç̉µ±Á½̀ơÖ±ÏßͬʱÏཻÓÚyÖáµÄ¸º°ëÖáÉϵĵăCʱ£¬Ç¡ºĂÓĐl1¡Íl2£¬¾¹ưµăA¡¢B¡¢CµÄÅ×ÎïÏߵĶԳÆÖáÓëÖ±Ïßl1½»ÓÚµăK£¬ÓëÖ±Ïßl2½»ÓÚµăE£¬ÔÚxÖá½»ÓÚµăF£¬DÊÇÅ×ÎïÏߵĶ¥µă£¬ÈçͼËùʾ£®·ÖÎö £¨1£©ÀûÓĂ¡÷BOC¡×¡÷COA£¬¸ù¾ƯÏàËÆÈư½ÇĐεÄĐÔÖÊÇóµĂOCµÄ³¤£¬ỘCµÄ×ø±ê¼´¿ÉÇóµĂ£¬È»ºóÀûÓĂ´ư¶¨ÏµÊư·¨ÇóµĂ¶₫´Îº¯ÊưµÄ½âÎöʽ£»
£¨2£©Ê×ÏÈÇóµĂl1£¬l2ºÍÅ×ÎïÏߵĶԳÆÖáµÄ½âÎöʽ£¬½ø¶øÇóµĂK¡¢D¡¢E¡¢F·Ö×ø±ê£¬ỘDK¡¢DE¡¢ºÍEFµÄ¹Øϵ¼´¿ÉÇóµĂ£»
£¨3£©·Ö³ÉK¡¢C¡¢M·Ö±đÊǵÈÑüÈư½ÇĐεĶ¥µăÈưÖÖÇé¿ö½øĐĐ̀ÖÂÛ£¬¸ù¾ƯµÈÑüÈư½ÇĐεÄĐÔÖÊÇó½â£®
½â´đ ½â£º£¨1£©ÓÉ̀ẩâ¿ÉµĂAO=1£¬BO=3£¬
¡ß¡÷BOC¡×¡÷COA£¬
¡à$\frac{CO}{BO}$=$\frac{AO}{CO}$£¬¼´$\frac{CO}{3}$=$\frac{1}{CO}$£¬
¡àCO=$\sqrt{3}$»̣-$\sqrt{3}$£¨ÉáÈ¥£©£®
¡àCµÄ×ø±êÊÇ£¨0£¬-$\sqrt{3}$£©£®
ÉèÅ×ÎïÏߵĽâÎöʽÊÇy=ax2+bx+c£¬
¸ù¾ỪẩâµĂ£º$\left\{\begin{array}{l}{a-b-c=0}\\{9a+3b+c=0}\\{c=-\sqrt{3}}\end{array}\right.$£¬
½âµĂ£º$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\\{c=-\sqrt{3}}\end{array}\right.$£¬
ỘÅ×ÎïÏߵĽâÎöʽÊÇy=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$£»
£¨2£©ËùµĂµÄÈừơÏ߶εÄÊưÁ¿¹ØϵÊÇKD=DE=EF£®
ÀíÓÉÊÇ£ºÉèÖ±Ïßl1µÄ½âÎöʽÊÇy=kx+b£¬
Ộ$\left\{\begin{array}{l}{-k+b=0}\\{b=-\sqrt{3}}\end{array}\right.$£¬
½âµĂ£º$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=-\sqrt{3}}\end{array}\right.$£¬
ỘÖ±Ïßl1µÄ½âÎöʽÊÇy=-$\sqrt{3}$x-$\sqrt{3}$£®
ͬÀíl2µÄ½âÎöʽÊÇy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$£®
Å×ÎïÏߵĶԳÆÖáÊÇx=1£¬
ỘKµÄ×ø±êÊÇ£¨1£¬-2$\sqrt{3}$£©£¬DµÄ×ø±êÊÇ£¨1£¬-$\frac{4\sqrt{3}}{3}$£©£¬EµÄ×ø±êÊÇ£¨1£¬-$\frac{2\sqrt{3}}{3}$£©£¬FµÄ×ø±êÊÇ£¨1£¬0£©£®
ỘKD=$\frac{2\sqrt{3}}{3}$£¬DE=$\frac{2\sqrt{3}}{3}$£¬EF=$\frac{2\sqrt{3}}{3}$£®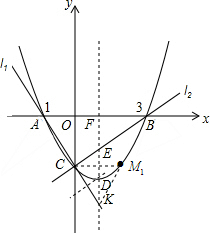
ỘKD=DE=EF£»
£¨3£©ÓÉ̀ẩâĐè½øĐĐ·ÖÀà̀ÖÂÛ£®
¢Ù̉ÔKΪԲĐÄ£¬KCµÄ³¤Îª°ë¾¶»Ô²»¡£¬½»Å×ÎïÏßÓÚµăM1£¬´ËʱKM1=KC£¬ỘM1ÓëC¹ØÓÚ¶Ô³ÆÖáx=1¶Ô³Æ£®
ÉèM1µÄºá×ø±êÊÇa£¬Ộ$\frac{1}{2}$a=1£¬½âµĂ£ºa=2£®
ỘM1µÄ×ø±êÊÇ£¨2£¬-$\sqrt{3}$£©£»
¢Úµ±̉ÔµăCΪԲĐÄ£¬Ï߶ÎKCµÄ³¤Îª°ë¾¶»Ô²»¡Ê±£¬ÓëÅ×ÎïÏߵĽ»µăM1ºÍA£¬¶øA¡¢C¡¢KÈưµăÔÚ̉»̀ơÖ±ÏßÉÏ£¬²»Äܹ¹³ÉÈư½ÇĐΣ»
¢Û×÷Ï߶ÎKCµÄÖĐ´¹Ïߣ¬
¡ßCD=$\sqrt{{1}^{2}+£¨-\sqrt{3}+\frac{4\sqrt{3}}{3}£©^{2}}$=$\frac{2\sqrt{3}}{3}$£¬
¡àCD=DK£®
¡àKCµÄÖĐ´¹Ïß̉»¶¨¾¹ưD£®
¼´´ËʱD¾ÍÊÇËùÇóµÄµăM2£®´ËʱÓеăM2£¬¼´µăM2µÄ×ø±êÊÇ£¨1£¬-$\frac{4\sqrt{3}}{3}$£©Ê¹µĂ¡÷M2CKÊǵÈÑüÈư½ÇĐΣ®
×ÛÉÏËùÊö£¬µ±µăMµÄ×ø±êÊÇ£¨2£¬-$\sqrt{3}$£©£¬£¨1£¬-$\frac{4\sqrt{3}}{3}$£©Ê±£¬¡÷MCKÊǵÈÑüÈư½ÇĐΣ®
µăÆÀ ±¾̀âÊÇ´ư¶¨ÏµÊư·¨Çóº¯Êư½âÎöʽ¡¢ÏàËÆÈư½ÇĐεÄĐÔÖỂÔ¼°µÈÑüÈư½ÇĐεÄÅж¨ÓëĐÔÖÊ£¬¶ÔµÈÑüÈư½ÇĐνøĐĐ̀ÖÂÛÊǽâ¾ö±¾̀âµÄ¹Ø¼ü£®


 ¿ÚËăĐÄËăËÙËăÓ¦ÓẰâϵÁĐ´đ°¸
¿ÚËăĐÄËăËÙËăÓ¦ÓẰâϵÁĐ´đ°¸ ͬ²½ÍØƠ¹ÔĶÁϵÁĐ´đ°¸
ͬ²½ÍØƠ¹ÔĶÁϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
 Èçͼ£¬Å×ÎïÏßy=$\frac{1}{2}$x2+bx-2ÓëxÖá½»ÓÚA¡¢BÁ½µă£¬ÓëyÖá½»ÓÚCµă£¬Ç̉A£¨-1£¬0£©£¬µăM£¨m£¬0£©ÊÇxÖáÉϵÄ̉»¸ö¶¯µă£¬
Èçͼ£¬Å×ÎïÏßy=$\frac{1}{2}$x2+bx-2ÓëxÖá½»ÓÚA¡¢BÁ½µă£¬ÓëyÖá½»ÓÚCµă£¬Ç̉A£¨-1£¬0£©£¬µăM£¨m£¬0£©ÊÇxÖáÉϵÄ̉»¸ö¶¯µă£¬²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 1 | B£® | 2 | C£® | 3 | D£® | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
 Èçͼ£¬¡÷ABCÖĐ£¬¡ÏABC=28¡ă£¬¡ÏC=32¡ă£¬BD¡ÍAC£¬´¹×ăΪD£¬AEƽ·Ö¡ÏBAC½»BDÑÓ³¤ÏßÓÚµăF£®Çó¡ÏBFEµÄ¶ÈÊư£®
Èçͼ£¬¡÷ABCÖĐ£¬¡ÏABC=28¡ă£¬¡ÏC=32¡ă£¬BD¡ÍAC£¬´¹×ăΪD£¬AEƽ·Ö¡ÏBAC½»BDÑÓ³¤ÏßÓÚµăF£®Çó¡ÏBFEµÄ¶ÈÊư£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 2x3+5x-1ºÍ-9x3-3x-3 | B£® | 5x3+x+8ºÍ-12x3+x-12 | ||
| C£® | -3x3+x+5ºÍ-4x3+x-1 | D£® | -7x3+3x-2ºÍ-x-2 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com