
【题目】在平面直角坐标系内,抛物线![]() 与线段
与线段![]() 有两个不同的交点,其中点
有两个不同的交点,其中点![]() ,点
,点![]() .有下列结论:
.有下列结论:
①直线![]() 的解析式为
的解析式为![]() ;②方程
;②方程![]() 有两个不相等的实数根;③a的取值范围是
有两个不相等的实数根;③a的取值范围是![]() 或
或![]() .
.
其中,正确结论的个数为( )
A.0B.1C.2D.3
【答案】D
【解析】
①设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,点
,点![]() 代入即可得到答案;
代入即可得到答案;
②∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,令
有两个不同的交点,令![]() x+
x+![]() =ax2x+1,则
=ax2x+1,则![]() 即可得到结论;
即可得到结论;
③分a>0,a<0两种情况讨论,根据题意列出不等式组,可求a的取值范围.
解:①设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,点
,点![]() 代入得,
代入得,
![]() 解得,
解得,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,故①正确;
,故①正确;
②∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
令![]() x+
x+![]() =ax2x+1,则
=ax2x+1,则![]() ,
,
∴方程![]() 有两个不相等的实数根,故②正确;
有两个不相等的实数根,故②正确;
③∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
∴令![]() x+
x+![]() =ax2x+1,则2ax23x+1=0
=ax2x+1,则2ax23x+1=0
∴Δ=98a>0
∴a<![]()
a<0时,![]()
解得:a2
∴a2,
当a>0时,![]()
解得:a1
∴1a<![]()
综上所述:1a<![]() 或a2, 故③正确.
或a2, 故③正确.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
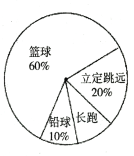
【题目】响应“阳光体育运动”号召,初三某班同学利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;进球数的中位数为 个,众数为 个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
查看答案和解析>>
科目:初中数学 来源: 题型:
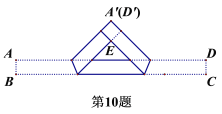
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
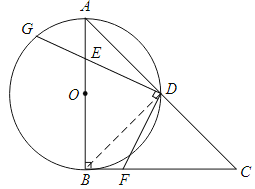
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
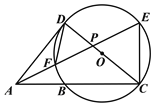
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
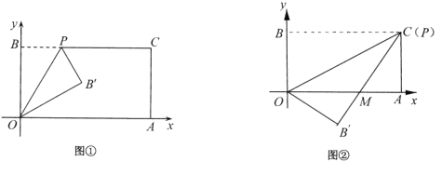
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
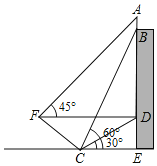
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
与坐标轴分别相交于点A、B,点C在线段AO上,点D在线段AB上,且AC=AD.将△ACD沿直线CD翻折得到△ECD.
(1)求AB的长;
(2)求证:四边形ACED是菱形;
(3)设点C的坐标为(0,![]() ),△ECD与△AOB重合部分的面积为
),△ECD与△AOB重合部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
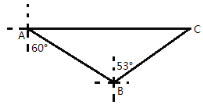
【题目】知识改变世界,科技改变生活。导航设备的不断更新方便了人们的出行。如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位)
(参考数据![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com