���𰸡�
��������1����Rt��ACF��Rt��BAO����CF=

OA=

t���ɴ����CF��ֵ��
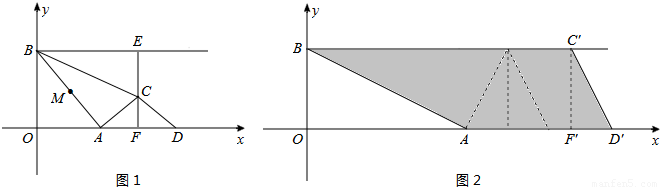
��2������Rt��ACF��Rt��BAO���������AF�ij��ȣ�����C�����߶�BD�ϣ����С�DCF�ס�DBO���������Ʊ���ʽ�з������t��ֵ��
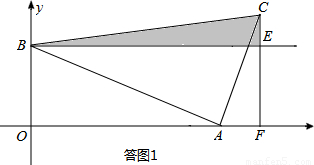
���������������Ҫ�������ۣ���0��t��8ʱ������ͼ1��ʾ����t��8ʱ�����ͼ1��ʾ��
��3�������漰ͼ�εļ�ƴ���ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣���Ҫ�������ۣ��ֱ����ͼ2-4��ʾ��
����⣺��1�������⣬��֤Rt��ACF��Rt��BAO��
��
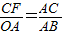
��
��AB=2AM=2AC��
��CF=

OA=

t��
��t=2ʱ��CF=1��
��2�����ɣ�1��֪��Rt��ACF��Rt��BAO��
��
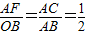
��
��AF=

OB=2����FD=AF=2����
�ߵ�C�����߶�BD�ϣ����DCF�ס�DBO��
��
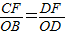
����

��
���t=
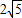
-2��t=-
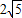
-2��С��0����ȥ��
�൱t=
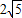
-2ʱ����C�����߶�BD�ϣ�
�ڵ�0��t��8ʱ������ͼ1��ʾ��
S=

BE•CE=

��t+2��•��4-

t��=
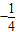
t
2+

t+4��
��t��8ʱ�����ͼ1��ʾ��
S=

BE•CE=

��t+2��•��

t-4��=

t
2-

t-4��
��3�����������ĵ�C������Ϊ����12��4������8��4����2��4����
�������£�
�ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣�
����һ�����ͼ2��ʾ����F��C��=AF��ʱ����F�������Ϊ��12��0����
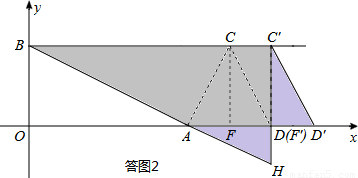
���ݡ�C��D��F��ա�AHF�䣬��BC��HΪƴ�ɵ������Σ���ʱC�������Ϊ��12��4����
�����������ͼ3��ʾ������F�����A�غ�ʱ����F�������Ϊ��8��0����
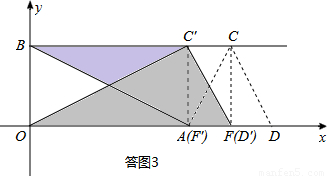
���ݡ�OC��A�ա�BAC�䣬��֪��OC��D��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��8��4����
����������BC��=F��D��ʱ����F�������Ϊ��2��0����

���ݡ�BC��H�ա�D��F��H����֪��AF��C��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��2��4����
���������⿼��������ƽ���ڼ���ͼ�εĶ������ʣ���һ���ѶȽϴ���п�ѹ���⣮�漰����֪ʶ��������������Ρ�ȫ�������Ρ�������ꡢ���α任����ת��ƽ�ơ��Գƣ���ͼ�εļ�ƴ���ⷽ�̵ȣ��dz�ȫ�棻�������۵�˼��ᴩ�ڣ�2�����ʺ͵ڣ�3���ʣ��ڣ�3���ʻ������˼���ͼ�εĿռ����������������漰�����ڶ࣬�ں��ḻ���Կ�������ѧ�ۺ�����Ҫ��ϸߣ�

 OA=
OA= t���ɴ����CF��ֵ��
t���ɴ����CF��ֵ��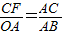 ��
�� OA=
OA= t��
t��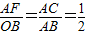 ��
�� OB=2����FD=AF=2����
OB=2����FD=AF=2����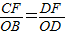 ����
���� ��
��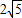 -2��t=-
-2��t=-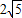 -2��С��0����ȥ��
-2��С��0����ȥ��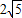 -2ʱ����C�����߶�BD�ϣ�
-2ʱ����C�����߶�BD�ϣ� BE•CE=
BE•CE= ��t+2��•��4-
��t+2��•��4- t��=
t��=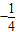 t2+
t2+ t+4��
t+4��
 BE•CE=
BE•CE= ��t+2��•��
��t+2��•�� t-4��=
t-4��= t2-
t2- t-4��
t-4��





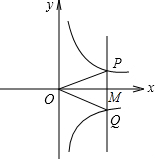 ��2012•���ʣ���ͼ������M��x��������������һ�㣬����M��PQ��y�ᣬ�ֱ���y=
��2012•���ʣ���ͼ������M��x��������������һ�㣬����M��PQ��y�ᣬ�ֱ���y=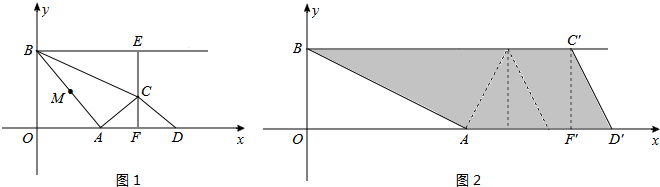
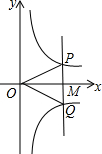 ��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y=
��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y= ��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y=
��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y= ��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y=
��ͼ������M��x���������ϵ�����һ�㣬����M��PQ��y�ᣬ�ֱ���y=