
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬·“±ČĄżŗÆŹżÓė¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó½»ÓŚµć
µÄĶ¼Ļó½»ÓŚµć![]() ŗĶµć
ŗĶµć![]() £®
£®
£Ø1£©µ±![]() Ź±£¬Ē󷓱ȥżŗÆŹżµÄ½āĪöŹ½£»
Ź±£¬Ē󷓱ȥżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ŅŃÖŖ¾¹żŌµćOµÄĮ½ĢõÖ±ĻßABÓėCD·Ö±šÓėĖ«ĒśĻß![]() ½»ÓŚA£¬BŗĶC£¬D£¬ÄĒĆ“ABÓėCD»„ĻąĘ½·Ö£¬ĖłŅŌĖıߊĪACBDŹĒĘ½ŠŠĖıߊĪĪŹ£ŗĘ½ŠŠĖıߊĪACBDÄÜ·ń³ÉĪŖ¾ŲŠĪ£æÄÜ·ń³ÉĪŖÕż·½ŠĪ£æČōÄÜ£¬ĒėĖµĆ÷Ļ߶ĪAB£¬CDµÄĪ»ÖĆ¹ŲĻµ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
½»ÓŚA£¬BŗĶC£¬D£¬ÄĒĆ“ABÓėCD»„ĻąĘ½·Ö£¬ĖłŅŌĖıߊĪACBDŹĒĘ½ŠŠĖıߊĪĪŹ£ŗĘ½ŠŠĖıߊĪACBDÄÜ·ń³ÉĪŖ¾ŲŠĪ£æÄÜ·ń³ÉĪŖÕż·½ŠĪ£æČōÄÜ£¬ĒėĖµĆ÷Ļ߶ĪAB£¬CDµÄĪ»ÖĆ¹ŲĻµ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©É趞“ĪŗÆŹżµÄĶ¼ĻóµÄ¶„µćĪŖQ£¬µ±”÷ABQŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪŹ±£¬ĒókµÄÖµ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©ÄܳÉĪŖ¾ŲŠĪ£¬²»ÄܳÉĪŖÕż·½ŠĪ£¬Ļ߶ĪABÓėCD»„ĻąĘ½·ÖĒŅĻąµČ£»£Ø3£©kµÄÖµĪŖ
£»£Ø2£©ÄܳÉĪŖ¾ŲŠĪ£¬²»ÄܳÉĪŖÕż·½ŠĪ£¬Ļ߶ĪABÓėCD»„ĻąĘ½·ÖĒŅĻąµČ£»£Ø3£©kµÄÖµĪŖ![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©Ö±½Ó°ŃµćA£Ø1£¬k£©“śČė·“±ČĄżŗÆŹżµÄ½āĪöŹ½¼“æÉ£¬ŌŁ°Ńk£½2“śČė¼“æÉ£»
£Ø2£©øł¾ŻA”¢CæÉŅŌĪŽĻŽ½Ó½ü×ų±źĻµµ«ŹĒ²»ÄÜĀäŌŚ×ų±źÖįÉĻ£¬¹ŹABÓėCDĪŽ·Ø“¹Ö±£¬¹ŹæÉµĆ³ö½įĀŪ£»
£Ø3£©ĻČ°Ńkµ±×÷ŅŃÖŖĢõ¼ž±ķŹ¾³öQµćµÄ×ų±ź£¬øł¾ŻA”¢B¹ŲÓŚŌµćOÖŠŠÄ¶Ō³ĘæÉÖŖµ±OQ£½OA£½OBŹ±£¬”÷ABQŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪ£¬ÓÉOQ2£½OA2£¬¼“æÉµĆ³ö¹ŲÓŚkµÄŅ»ŌŖ¶ž“Ī·½³Ģ£¬Ēó³ökµÄÖµ¼“æÉ£®
£Ø1£©![]() ·“±ČĄżŗÆŹżµÄĶ¼Ļó¹żµć
·“±ČĄżŗÆŹżµÄĶ¼Ļó¹żµć![]() £¬
£¬
![]() ·“±ČĄżŗÆŹżµÄ½āĪöŹ½ŹĒ
·“±ČĄżŗÆŹżµÄ½āĪöŹ½ŹĒ![]() £¬
£¬
µ±![]() Ź±£¬·“±ČĄżŗÆŹżµÄ½āĪöŹ½ŹĒ
Ź±£¬·“±ČĄżŗÆŹżµÄ½āĪöŹ½ŹĒ![]() £®
£®
£Ø2£©ÄܳÉĪŖ¾ŲŠĪ£¬²»ÄܳÉĪŖÕż·½ŠĪ£¬Ļ߶ĪABÓėCD»„ĻąĘ½·ÖĒŅĻąµČ£®
µ±AB£¬CD¹ŲÓŚÖ±Ļß![]() »ņ
»ņ![]() ¶Ō³ĘŹ±£¬ABÓėCD»„ĻąĘ½·ÖĒŅĻąµČ£¬
¶Ō³ĘŹ±£¬ABÓėCD»„ĻąĘ½·ÖĒŅĻąµČ£¬
![]() ĖıߊĪACBDÄܳÉĪŖ¾ŲŠĪ£®
ĖıߊĪACBDÄܳÉĪŖ¾ŲŠĪ£®
![]() µćA£¬B£¬C£¬DæÉŅŌĪŽĻŽ½Ó½ü×ų±źÖįµ«ŹĒ²»ÄÜĀäŌŚ×ų±źÖįÉĻ£¬
µćA£¬B£¬C£¬DæÉŅŌĪŽĻŽ½Ó½ü×ų±źÖįµ«ŹĒ²»ÄÜĀäŌŚ×ų±źÖįÉĻ£¬
![]() ABÓėCDĪŽ·Ø“¹Ö±£¬
ABÓėCDĪŽ·Ø“¹Ö±£¬
![]() ĖıߊĪACBD²»ÄܳÉĪŖÕż·½ŠĪ£®
ĖıߊĪACBD²»ÄܳÉĪŖÕż·½ŠĪ£®
£Ø3£©![]() ¶ž“ĪŗÆŹżµÄ¶„µćQµÄ×ų±źŹĒ
¶ž“ĪŗÆŹżµÄ¶„µćQµÄ×ų±źŹĒ![]() £¬A£¬B¹ŲÓŚŌµćOÖŠŠÄ¶Ō³Ę£¬
£¬A£¬B¹ŲÓŚŌµćOÖŠŠÄ¶Ō³Ę£¬
![]() µ±
µ±![]() Ź±£¬
Ź±£¬![]() ŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪ£®
ŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪ£®
ÓÉ![]() £¬µĆ
£¬µĆ £¬
£¬
½āµĆ![]() £¬
£¬![]() £¬
£¬
![]() µ±
µ±![]() ŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪŹ±£¬kµÄÖµĪŖ
ŹĒŅŌABĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪŹ±£¬kµÄÖµĪŖ![]() »ņ
»ņ![]() £®
£®


 ѧ¶ųÓÅĻĪ½Ó½Ģ²ÄÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ѧ¶ųÓÅĻĪ½Ó½Ģ²ÄÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø Š”ѧæĪĢĆ×÷ŅµĻµĮŠ“š°ø
Š”ѧæĪĢĆ×÷ŅµĻµĮŠ“š°ø ½š²©ŹæŅ»µćČ«ĶØĻµĮŠ“š°ø
½š²©ŹæŅ»µćČ«ĶØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() µÄ¶„µć
µÄ¶„µć![]() ŌŚĖ«ĒśĻß
ŌŚĖ«ĒśĻß![]() µÄĶ¼ĻóÉĻ£¬Ö±½Ē±ß
µÄĶ¼ĻóÉĻ£¬Ö±½Ē±ß![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬
ÖįÉĻ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄÖµŹĒ£Ø £©
µÄÖµŹĒ£Ø £©

A. 4![]() B. -4
B. -4![]() C. 2
C. 2![]() D. -2
D. -2![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
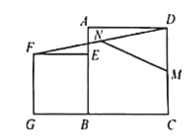
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćEŌŚÕż·½ŠĪABCDµÄ±ßABÉĻ£¬ŅŌBEĪŖ±ßĻņÕż·½ŠĪABCDĶā²æ×÷Õż·½ŠĪBEFG£¬Į¬½ÓDF£¬M”¢N·Ö±šŹĒDC”¢DFµÄÖŠµć£¬Į¬½ÓMN.ČōAB=7£¬BE=5£¬ŌņMN=_______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
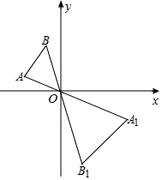
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷AOBŗĶ”÷A1OB1ŹĒŅŌµćOĪŖĪ»ĖĘÖŠŠÄµÄĪ»ĖĘĶ¼ŠĪ£¬ĒŅ”÷AOBŗĶ”÷A1OB1µÄÖܳ¤Ö®±ČĪŖ1£ŗ2£¬µćBµÄ×ų±źĪŖ£Ø-1£¬2£©£¬ŌņµćB1µÄ×ų±źĪŖ£Ø””””£©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»×éĮŚ±ßĻąµČµÄĶ¹ĖıߊĪ½Š×ö”°ŗĶÄĄĖıߊĪ”±£¬Ō¢ŅāŹĒČ«ŹĄ½ēŗĶĘ½¹²“¦£¬ÄĄĮŚÓŃŗĆ£¬¹²Ķ¬·¢Õ¹.ČēĮāŠĪ£¬Õż·½ŠĪµČ¶¼ŹĒ”°ŗĶÄĄĖıߊĪ”±.
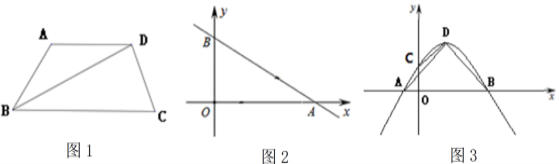
£Ø1£©ČēĶ¼1£¬BDĘ½·Ö”ĻABC£¬AD”ĪBC£¬ĒóÖ¤:ĖıߊĪABCDĪŖ”°ŗĶÄĄĖıߊĪ”±£»
£Ø2£©ČēĶ¼2£¬Ö±Ļß![]() ÓėxÖį”¢yÖį·Ö±š½»ÓŚA”¢BĮ½µć£¬µćP”¢Q·Ö±šŹĒĻ߶ĪOA”¢ABÉĻµÄ¶Æµć.µćP“ÓµćA³ö·¢,ŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµćOŌĖ¶Æ.µćQ“ÓµćA³ö·¢,ŅŌĆæĆė5øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµćBŌĖ¶Æ.P”¢QĮ½µćĶ¬Ź±³ö·¢£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė.µ±ĖıߊĪBOPQĪŖ”°ŗĶÄĄĖıߊĪ”±Ź±£¬ĒótµÄÖµ£»
ÓėxÖį”¢yÖį·Ö±š½»ÓŚA”¢BĮ½µć£¬µćP”¢Q·Ö±šŹĒĻ߶ĪOA”¢ABÉĻµÄ¶Æµć.µćP“ÓµćA³ö·¢,ŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµćOŌĖ¶Æ.µćQ“ÓµćA³ö·¢,ŅŌĆæĆė5øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµćBŌĖ¶Æ.P”¢QĮ½µćĶ¬Ź±³ö·¢£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė.µ±ĖıߊĪBOPQĪŖ”°ŗĶÄĄĖıߊĪ”±Ź±£¬ĒótµÄÖµ£»
£Ø3£©ČēĶ¼3£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµć
Öį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµć![]() £¬Å×ĪļĻߵĶ„µćĪŖµćD.µ±ĖıߊĪCOBDĪŖ”°ŗĶÄĄĖıߊĪ”±£¬ĒŅCD=OC.Å×ĪļĻß»¹Āś×ć£ŗ¢Ł
£¬Å×ĪļĻߵĶ„µćĪŖµćD.µ±ĖıߊĪCOBDĪŖ”°ŗĶÄĄĖıߊĪ”±£¬ĒŅCD=OC.Å×ĪļĻß»¹Āś×ć£ŗ¢Ł![]() £»¢Ś¶„µćDŌŚŅŌABĪŖÖ±¾¶µÄŌ²ÉĻ. µć
£»¢Ś¶„µćDŌŚŅŌABĪŖÖ±¾¶µÄŌ²ÉĻ. µć![]() ŹĒÅ×ĪļĻß
ŹĒÅ×ĪļĻß![]() ÉĻČĪŅāŅ»µć£¬ĒŅ
ÉĻČĪŅāŅ»µć£¬ĒŅ![]() .Čō
.Čō![]() ŗć³ÉĮ¢£¬ĒómµÄ×īŠ”Öµ.
ŗć³ÉĮ¢£¬ĒómµÄ×īŠ”Öµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢ŁŹĒŅ»ÖÖ°ü×°ŗŠµÄ±ķĆęÕ¹æŖĶ¼£¬½«ĖüĪ§ĘšĄ“æɵƵ½Ņ»øö¼øŗĪĢåµÄÄ£ŠĶ£®
(1)ĒėĖµ³öÕāøö¼øŗĪĢåÄ£ŠĶµÄ×īČ·ĒŠµÄĆū³ĘŹĒ__ __£»
(2)ČēĶ¼¢ŚŹĒøł¾Ż a£¬hµÄȔֵ»³öµÄ¼øŗĪĢåµÄÖ÷ŹÓĶ¼ŗĶø©ŹÓĶ¼(Ķ¼ÖŠµÄ“ÖŹµĻß±ķŹ¾µÄÕż·½ŠĪ(ÖŠ¼äŅ»ĢõŠéĻß)ŗĶČż½ĒŠĪ)£¬ĒėŌŚĶųøńÖŠ»³öøĆ¼øŗĪĢåµÄ×óŹÓĶ¼£»
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬ŅŃÖŖh£½20 cm£¬ĒóøĆ¼øŗĪĢåµÄ±ķĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĀ·µĘĻĀ£¬Š”Ć÷µÄÉķøßČēĶ¼ÖŠĻ߶ĪABĖłŹ¾£¬ĖūŌŚµŲĆęÉĻµÄÓ°×ÓČēĶ¼ÖŠĻ߶ĪACĖłŹ¾£¬Š”ĮĮµÄÉķøßČēĶ¼ÖŠĻ߶ĪFGĖłŹ¾£¬Ā·µĘµĘÅŻŌŚĻ߶ĪDEÉĻ£®

£Ø1£©ĒėÄćČ·¶ØµĘÅŻĖłŌŚµÄĪ»ÖĆ£¬²¢»³öŠ”ĮĮŌŚµĘ¹āĻĀŠĪ³ÉµÄÓ°×Ó£®
£Ø2£©Čē¹ūŠ”Ć÷µÄÉķøßAB=1.6m£¬ĖūµÄÓ°×Ó³¤AC=1.4m£¬ĒŅĖūµ½Ā·µĘµÄ¾ąĄėAD=2.1m£¬ĒóµĘÅŻµÄøß.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćA£Ø3£¬3£©£¬µćB£Ø4£¬0£©£¬µćC£Ø0£¬©1£©£®

£Ø1£©ŅŌµćCĪŖÖŠŠÄ£¬°Ń”÷ABCÄꏱÕėŠż×Ŗ90”ć£¬ĒėŌŚĶ¼ÖŠ»³öŠż×ŖŗóµÄĶ¼ŠĪ”÷A”äB”äC£¬µćB”äµÄ×ų±źĪŖ________£»
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬Ēó³öµćA¾¹żµÄĀ·¾¶![]() µÄ³¤£Ø½į¹ū±£Įō¦Š£©£®
µÄ³¤£Ø½į¹ū±£Įō¦Š£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
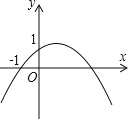
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóµÄ¶„µćŌŚµŚŅ»ĻóĻŽ£¬ĒŅ¹żµć£Ø0£¬1£©ŗĶ£Ø©1£¬0£©£®ĻĀĮŠ½įĀŪ£ŗ¢Łab£¼0£¬¢Śb2£¾4a£¬¢Ū0£¼a+b+c£¼2£¬¢Ü0£¼b£¼1£¬¢Żµ±x£¾©1Ź±£¬y£¾0£¬ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ
A£®5øö B£®4øö C£®3øö D£®2øö
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com