(1)解:B点坐标为(2,2),四边形OABC是正方形,
∴点A(0,2),C(2,0),
∵抛物线y=

x
2+bx+c经过点A、C,
∴
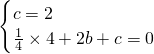
,
解得
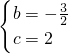
,
∴抛物线解析式为y=

x
2-

x+2;
根据垂径定理,AB的垂直平分线与x轴的交点为圆心P,即P(1,0),
如图,连接PE、PA,则PE
2=PA
2=OA
2+OP
2=2
2+1
2=5,
设正方形CDEF的边长为a,
则PF=a+1,
在Rt△PEF中,PE
2=PF
2+EF
2,
即5=(a+1)
2+a
2,
整理得,a
2+a-2=0,
解得a
1=1,a
2=-2(舍去),
∴OF=OC+CF=2+1=3,
∴点E的坐标为(3,1);
(2)证明:令y=0,则

x
2-

x+2=0,
整理得,x
2-6x+8=0,
解得x
1=2,x
2=4,
∴点G的坐标为(4,0),
∴点M是FG的中点,
∴点M(3.5,0),
∴FM=3.5-3=0.5,
PM=3.5-1=2.5,
在Rt△EFM中,EM
2=EF
2+FM
2=1
2+0.5
2=

,
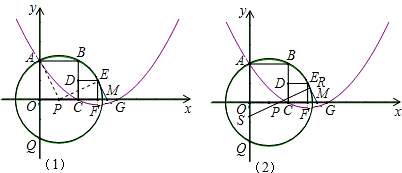
∴PE
2+EM
2=5+

=

,
∵PM
2=2.5
2=

,
∴PE
2+EM
2=PM
2,
∴△PEM是直角三角形,且PE⊥EM,
∴ME是⊙P的切线;
(3)解:不变,面积为

.
理由如下:∵圆心P在x轴上,点A的坐标为(0,2),
∴点Q的坐标为(0,-2),
∵点R的速度为1个单位/秒,点S的速度为5个单位/秒,
∴点R(3,1-t),S(0,5t-2),
设直线RS的解析式为y=mx+n,
则
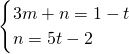
,
解得
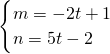
,
所以,直线RS的解析式为y=(-2t+1)x+5t-2,
当x=2时,y=(-2t+1)×2+5t-2=-4t+2+5t-2=t,
又∵RF=1-t,
∴正方形CDEF在直线RS下方部分的面积=

[t+(1-t)]×1=

,与t无关,是定值,
即正方形CDEF在直线RS下方部分的面积不变,为

.
分析:(1)根据点B的坐标以及正方形的性质求出点A、C的坐标,然后利用待定系数法求二次函数解析式解答;根据垂径定理可得圆心P为AB的垂直平分线与x轴的交点,连接PE、PA,根据勾股定理表示出PA
2,设正方形CDEF的边长为a,表示出PF,然后在Rt△PEF中,利用勾股定理列式进行计算即可求出a的值,然后求出OF,即可得到点E的坐标;
(2)令y=0,利用抛物线解析式求出点G的坐标,然后得到点M的坐标,再求出FM、PM,然后利用勾股定理逆定理判定PE⊥EM,再根据切线的定义得证;
(3)表示出点S、R的坐标,然后利用待定系数法求一次函数解析式求出直线SR的解析式,再求出SR与CD的交点坐标,然后根据梯形的面积公式列式进行计算即可求出正方形CDEF在直线RS下方部分的面积为定值.
点评:本题是二次函数综合题型,主要考查了正方形的性质,待定系数法求函数解析(包括二次函数解析式,一次函数解析式),勾股定理的应用,圆的切线的判定,(3)的求解较为巧妙,利用直线RS的解析式确定与CD的交点是解题的关键.

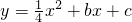 经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).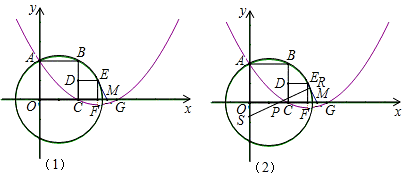
 x2+bx+c经过点A、C,
x2+bx+c经过点A、C,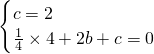 ,
,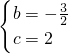 ,
, x2-
x2- x+2;
x+2; x2-
x2- x+2=0,
x+2=0, ,
,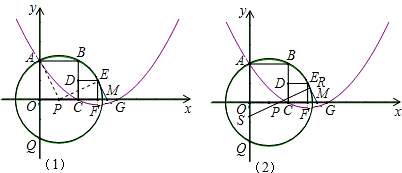
 =
= ,
, ,
, .
.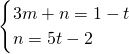 ,
,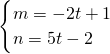 ,
, [t+(1-t)]×1=
[t+(1-t)]×1= ,与t无关,是定值,
,与t无关,是定值, .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
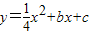 经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
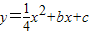 经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
 经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
经过A、C两点,与x轴的另一交点为G,M是FG的中点,B点坐标为(2,2).