
【题目】如图①线段![]() 是
是![]() 的直径,
的直径,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 不与点
不与点![]() 重合),直径
重合),直径![]() 的垂线
的垂线![]() 与
与![]() 的平行线
的平行线![]() 相交于点
相交于点![]() 连接
连接![]() 设
设![]()
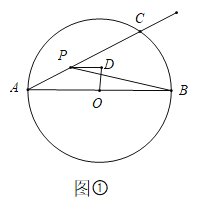
![]() 求
求![]() 的取值范围;
的取值范围;
![]() 如图②点
如图②点![]() 是线段
是线段![]() 与
与![]() 的交点,若
的交点,若![]() 求证:直线
求证:直线![]() 与
与![]() 相切;
相切;

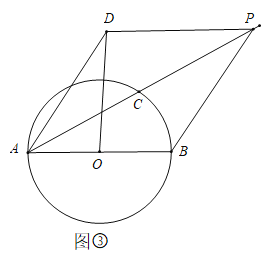
![]() 如图③当
如图③当![]() 时,连接
时,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)x≥2;(2)证明见解析;(3)四边形![]() 为菱形,理由见解析.
为菱形,理由见解析.
【解析】
(1)当点P在点C处,PB取得最小值,即x=![]() AB=2,即可求解;
AB=2,即可求解;
(2)若证明线段PD与⊙O相切,可证明![]() 且OD=OA=2,连接
且OD=OA=2,连接![]() 过点
过点![]() 作
作![]() 于点
于点![]() 先求得PH和AP,即可求得OD.
先求得PH和AP,即可求得OD.
(3)先证得![]() ,求得AP和IA,
,求得AP和IA,![]() ,求得
,求得![]() ,故得DP,DP=AB,且
,故得DP,DP=AB,且![]() 可证得四边形
可证得四边形![]() 为平行四边形,又因为
为平行四边形,又因为![]() =PB,所以四边形
=PB,所以四边形![]() 为菱形.
为菱形.
(1)如图所示,当点![]() 与
与![]() 重合时,
重合时,![]() 最短.
最短.
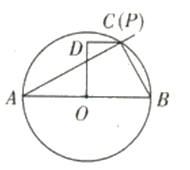
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
故答案为:![]()
(2)如图所示:连接![]() 过点
过点![]() 作
作![]() 于点
于点![]()
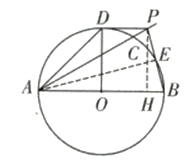
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() .
.
∵![]()
∴![]()
∴![]() .
.
在![]() 中,
中,![]()
∴![]() .
.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴直线![]() 与⊙O相切;
与⊙O相切;
(3)四边形![]() 为菱形.
为菱形.
理由如下:
如图所示:连接![]() 与
与![]() 相交于点
相交于点![]() ,
,
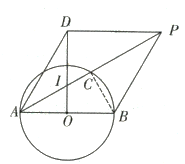
∵![]() 是⊙O的直径
是⊙O的直径
∴![]()
∵![]()
∴![]()
∴![]() .
.
在![]() 中,
中,![]()
∴![]() .
.
∴在![]() 中,
中,![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]() .
.
又∵![]()
∴四边形![]() 为平行四边形
为平行四边形
∵![]()
∴四边形![]() 为菱形.
为菱形.


科目:初中数学 来源: 题型:
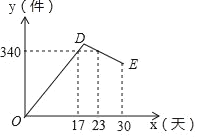
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离![]() 与小王的行驶时间
与小王的行驶时间![]() 之间的函数关系.
之间的函数关系.
请你根据图象进行探究:
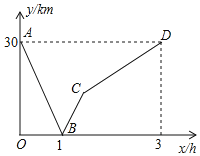
(1)小王和小李的速度分别是多少?
(2)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年3月16日,由中国科协主办的第六届全国青年科普创新实验暨作品大赛启动,重点围绕“智能、环保、教育”三大主题,某中学派出甲、乙两组队伍参加本次大赛,有四个命题供他们选择:
①智能:智能控制及人工智能命题(用![]() 表示)
表示)
②环保:包括生物环境、风能两个命题(分别用![]() 表示)
表示)
③教育:未来教育命题(用![]() 表示)
表示)
![]() 甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
![]() 若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ACB=90°,D在斜边AB上,DE⊥AC,DF⊥BC,垂足分别为E,F.
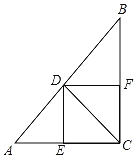
(1)当∠ACD=∠BCD时,求证:四边形DECF是正方形;
(2)当∠BCD=∠A时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
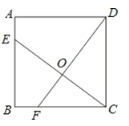
【题目】如图,已知正方形ABCD的边长为4,点E.F分别在边AB.BC上,且AE=BF=1,CE.DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=![]() ,④S△ODC=S四边形BEOF中,正确的有_______________________.
,④S△ODC=S四边形BEOF中,正确的有_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
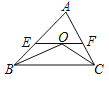
【题目】如图,在![]() 中,
中, ![]() 是
是![]() 平分线的交点,过点O作
平分线的交点,过点O作![]() ,分别交
,分别交![]() 于点
于点![]() ,已知
,已知![]() (
(![]() 常数) ,设
常数) ,设![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,在下列图像中,大致表示
,在下列图像中,大致表示![]() 与
与![]() 之间的函数关系式的是( )
之间的函数关系式的是( )
A. B.
B.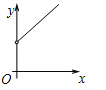 C.
C.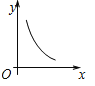 D.
D.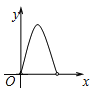
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com