
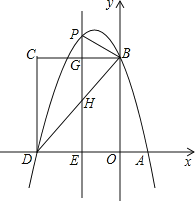
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣3x+4;(2)PG=﹣m2﹣3m,(3)m=﹣2
【解析】
(1)将A(1,0),B(0,4)代入y=﹣x2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)先求出抛物线与直线BC的交点为(﹣2,4)(0,4),得出点P在直线BC上方时,m的取值范围,再根据P(m,﹣m2﹣3m+4),G(m,4),求出PG=﹣m2﹣m;
(3)先求出直线BD的解析式,进而求出H的坐标,然后分两种情况![]() 和
和![]() 进行讨论即可.
进行讨论即可.
解:(1)∵点A和点B在抛物线上, 将A(1,0),B(0,4)代入y=﹣x2+bx+c得
![]() 解得
解得![]()
∴该抛物线的解析式为:y=﹣x2﹣3x+4;
(2)∵4=﹣m2﹣3m+4,解得m=﹣3或0,
∴抛物线与直线BC的交点为(﹣3,4)(0,4),
∴点P在直线BC上方时,m的取值范围是:﹣3<m<0,
∵E(m,0),B(0,4),
∵PE⊥x轴交抛物线于点P,交BC于点G,
∴P(m,﹣m2﹣3m+4),G(m,4),
∴PG=﹣m2﹣3m+4﹣4=﹣m2﹣3m,
(3)∵y=﹣x2﹣3x+4;
∴当y=0时,![]() 或-4
或-4
![]()
设直线BD的解析式为![]()
将B,D两点代入![]() 中,得
中,得
![]() 解得
解得![]()
∴直线BD的解析式为![]()
![]()
①若![]() ,那么
,那么![]()
即![]()
∴m=﹣2或m=0
∵﹣3<m<0故m=﹣2
②若![]() ,那么
,那么![]()
即![]()
∴m=﹣2或m=0
∵﹣3<m<0故m=﹣2
综上所述,m=﹣2


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
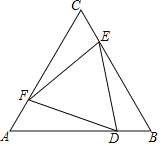
【题目】如图,一张正三角形的纸片的边长为2cm,D、E、F分别是边AB、BC、CA(含端点)上的点,设BD=CE=AF=x(cm),△DEF的面积为y(cm2).
(1)求y关于x的函数表达式和自变量的取值范围;
(2)求△DEF的面积y的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,点E落在AD边上,若AF=4.AB=7.
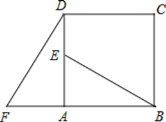
(1)旋转中心为 ;旋转角度为 ;
(2)求DE的长度;
(3)指出BE与DF的关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
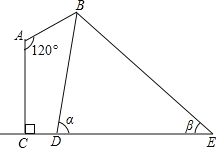
【题目】如图是某路灯在铅锤面内的示意图,灯柱AC的高为15.25米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为22米,从D、E两处测得路灯B的仰角分别为α和β,且tanα=8,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
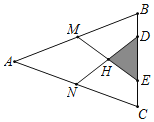
【题目】在△ABC中,AB=AC=13cm,BC=10cm,M、N分别是AB、AC的中点,D、E在BC上,且DE=5cm,连结DN、ME交于H,则△HDE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.
(1)按这种方法组成两位数45是_____事件,填(“不可能”、“随机”、“必然”)
(2)组成的两位数能被3整除的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0; ②b2-4ac<0 ; ③2a+b>0 ;④a+b+c>0,其中正确的个数( )
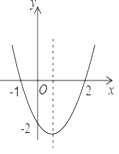
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
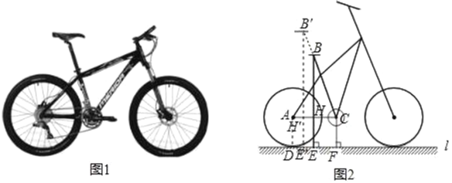
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,
∠AOD=∠APC.
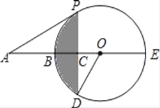
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com