Question

在Rt△ABC和Rt△A′B′C′中，∠ACB=∠A′C′B′=90°．

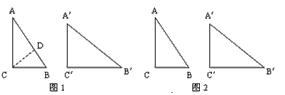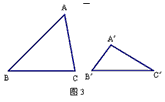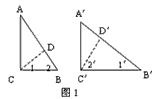
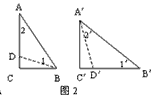
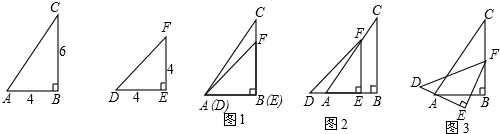
（1）如图1，分割线CD将Rt△ABC分割成两个三角形△ADC和△BDC，且满足∠BCD=∠B′．试在Rt△A′B′C′的内部也作一条类似的分割线，使这条分割线把Rt△A′B′C′分得的两个三角形分别与△ADC和△BDC相似，并说明你画法的正确性（作图工具不限，下同）； （2）请在图2中画出与图1中不同的两条分割线，使得Rt△ABC被分得的两个三角形与Rt△A′B′C′被分得的两个三角形分别相似（直接画出分割线，写出相似三角形，不必说明理由）； （3）如图3，已知任意△ABC和△A′B′C′，试分别在△ABC和△A′B′C′中画1条或两条分割线，使得△ABC被分得的若干个三角形分别与△A′B′C′被分得的若干个三角形相似（直接画出分割线，相等的角分别在图中用∠1、∠1′，∠2、∠2′，∠3、∠3′，……对应地标明，并写出所有相似三角形，不必说明理由）． （4）由上面的操作，你得到什么一般性的经验?

Answer 1

（1）如图1，∠1=∠1′，作∠2′=∠2， 所以△ADC∽△C′D′A′和△BDC∽△C′D′B′，    由两角对应相等的两个三角形相似即可证得； （2）如图2，若△ABC∽△A′B′C′，可有多种方法分割， 这里不妨设∠ABC＞∠A′B′C′，在∠ABC的内部作 ∠1=∠1′， 在∠B′A′C′的内部作∠2′=∠2 (画法不惟一) ， 则△ADB∽△A′D′B′和△BDC∽△A′D′C′； （3）如图3，若△ABC∽△A′B′C′，可有多种方法分割， 这里不妨设∠ACB＞∠A′C′B′，∠B′A′C′＞∠BAC， 在∠ACB的内部作∠1=∠1′，在∠B′A′C′的内部作∠2′ =∠2， 因此△ADC∽△A′D′C′；这样我们可以仿照（2）继续将 △DBC和△A′B′D′进行分割，作∠3=∠3′， ∠4′=∠4，这样， △ADC∽△A′D′C′， △BED∽△D′E′BC′， △DEC∽△A′E′D′； (画法不惟一) （4）由上面的操作可知，对任意两个三角形，我们都可以通过 适当的方法将每个三角形分割成n(n≥2)个三角形，并且可 使这n对三角形一一相似