
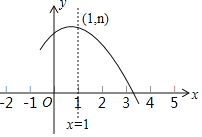
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①4a﹣2b+c>0;②3a+b>0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个互异实根.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
根据二次函数图象和性质,开口向下,可得a<0,对称轴x=1,利用顶点坐标,图象与x轴的交点情况,对照选项逐一分析即可.
①∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间,
∴当x=﹣2时,y<0,
即4a﹣2b+c<0,所以①不符合题意;
②∵抛物线的对称轴为直线x=﹣![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴3a+b=3a﹣2a=a<0,所以②不符合题意;
③∵抛物线的顶点坐标为(1,n),
∴![]() =n,
=n,
∴b2=4ac﹣4an=4a(c﹣n),所以③符合题意;
④∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n﹣1有2个公共点,
∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④符合题意.
故选:B.


科目:初中数学 来源: 题型:
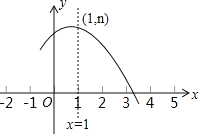
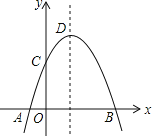
【题目】如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①抛物线的对称轴是直线x=1;
②若OC=OB,则c=2;
③若M(x0,y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.其中真命题个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
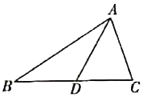
(1)如图,![]() 是
是![]() 的中线,则
的中线,则![]() __________
__________![]() ;(填“
;(填“![]() ”“
”“![]() ”或“
”或“![]() ”)
”)
问题探究
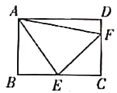
(2)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,当
上任意一点,当![]() 的周长最小时,求
的周长最小时,求![]() 的长;
的长;
问题解决
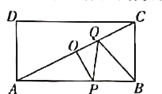
(3)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,点
上任意一点,点![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,是否存在这样的点
,是否存在这样的点![]() ,使折线
,使折线![]() 的长度最小?若存在,请确定点
的长度最小?若存在,请确定点![]() 的位置,并求出折线
的位置,并求出折线![]() 的最小长度;若不存在,请说明理由.
的最小长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
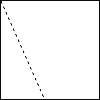
A.直角三角形B.平行四边形C.菱形D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,0<x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
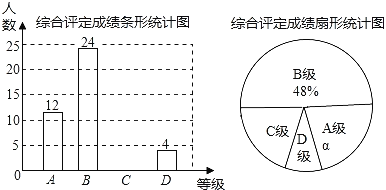
(1)在这次调查中,一共抽取了 名学生;
(2)扇形统计图中,α= %,C级对应的圆心角为 度;
(3)请你利用你所学的统计知识,估计本次抽取所有学生的综合评定成绩的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作弦
作弦![]() 垂直于直径
垂直于直径![]() 于
于![]() ,点
,点![]() 恰好为
恰好为![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
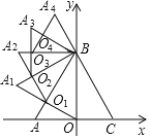
【题目】如图,边长为4的等边△ABC,AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边△OBA1,边OA1与AB交于点O1,以O1B为边作等边△O1BA2,边O1A2与A1B交于点O2,以O2B为边作等边△O2BA3,边O2A3与A2B交于点O3,…,依此规律继续作等边△On﹣1BAn,则![]() 的横坐标_____.
的横坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2020年元月起,收费标准上调为餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2020年处理的这两种垃圾数量与2019年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2019年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2020年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2020年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com