
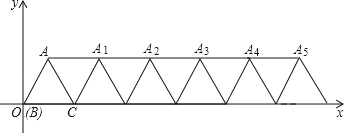
【题目】如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°得到△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)点A的坐标为 ;点A1的坐标为 .
(2)A2018的坐标为 .
【答案】(1)(2,2![]() );(6,2
);(6,2![]() );(2)(8074,2
);(2)(8074,2![]() ).
).
【解析】
(1) 边长为4的等边△ABC的顶点B与原点重合,可得OA=BC=4,∠AOC=60°,过点A作AD⊥x轴于点D,求出A点坐标,再根据ABCA1是平行四边形得出A1的坐标;
(2)将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,最后得出A2018的坐标.
(1)∵边长为4的等边△ABC的顶点B与原点重合,
∴OA=BC=4,∠AOC=60°.
如图,过点A作AD⊥x轴于点D,
∴BD=DC=![]() BC=2,AD=2
BC=2,AD=2![]() ,
,
∴点A的坐标为(2,2![]() ).
).
∵将△ABC绕顶点C顺时针旋转60°得到△ACA1,
∴四边形ABCA1是平行四边形,
∴AA1=BC=4,AA1∥BC,
∴点A1的坐标为(2+4,2![]() ),即(6,2
),即(6,2![]() ).
).
故答案为:(2,2![]() );(6,2
);(6,2![]() ).
).
(2)∵将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,
∴点A2的坐标为(2+4×2,2![]() ),即(10,2
),即(10,2![]() );点A3的坐标为(2+4×3,2
);点A3的坐标为(2+4×3,2![]() ),即(14,2
),即(14,2![]() );……;
);……;
∴点A2018的坐标为(2+4×2018,2![]() ),即(8074,2
),即(8074,2![]() ).
).
故答案为:(8074,2![]() ).
).


科目:初中数学 来源: 题型:
【题目】2018年,某县为改善环境,方便居民出行,进行了路面硬化,计划经过几个月使城区路面硬化面积新增400万平方米.工程开始后,实际每个月路面硬化面积是原计划的2倍,这样可提前5个月完成任务.
(1) 求实际每个月路面硬化面积为多少万平方米?
(2) 工程开始2个月后,随着冬季来临,气温下降,县委、县政府决定继续加快路面硬化速度,要求余下工程不超过2个月完成,那么实际平均每个月路面硬化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题及点拨,补全解题过程(完成点拨部分的填空),并解决问题:
例题:如图1,在等边![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是
是![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.
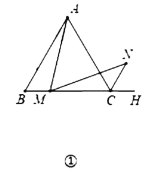

点拨:如图2,作![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,得等边
,得等边![]() ,连结
,连结![]() ,易证
,易证![]() (_______),可得
(_______),可得![]() ,
,![]() ;
;
又![]() ,则
,则![]() ,可得
,可得![]() ____
____![]() _____;
_____;
由![]() ,进一步可得
,进一步可得![]() ______;
______;
又因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
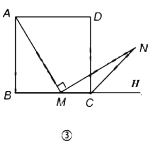
问题:如图3,四边形![]() 的四条边都相等,四个角都等于
的四条边都相等,四个角都等于![]() ,
,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是四边形
是四边形![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求
.求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程
(1)x2﹣4x+1=0 (2)(5x﹣3)2+2(3﹣5x)=0
(3)(2x+1)2=(x﹣1)2 (4)4x2+2=7x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
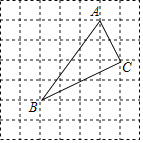
(1)建立适当的平面直角坐标系,使点A(3,4)、C(4,2),则点B的坐标为 ;
(2)求图中格点△ABC的面积;
(3)判断格点△ABC的形状,并说明理由.
(4)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴正半轴上.
轴正半轴上.



(1)![]() 的平分线与
的平分线与![]() 的外角平分线交于点
的外角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
(2)设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且满足
,且满足![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,请直接写出点
为斜边的等腰直角三角形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
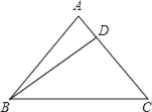
【题目】已知等腰三角形ABC的底边长BC=20cm,D是AC上的一点,且BD=16cm,CD=12cm.
(1)求证:BD⊥AC;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com