
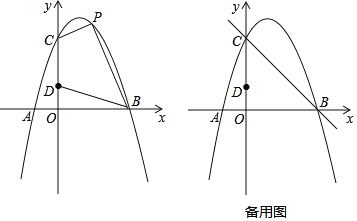
【题目】如图,对称轴为直线![]() 的抛物线经过
的抛物线经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求四边形
时,求四边形![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
②点![]() 在直线
在直线![]() 上,若以
上,若以![]() 为边,点
为边,点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请求出所有符合条件的点
为顶点的四边形是平行四边形,请求出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+2x+3;(2)①S=![]() ,S的最大值为
,S的最大值为![]() ;②点P的坐标分别为:P1(1,4),P2(2,3),P3(
;②点P的坐标分别为:P1(1,4),P2(2,3),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
(1)由对称轴和A点坐标可求出B点坐标,设抛物线的解析式为y=a(x+1)(x-3),把C(0,3)代入,可求出a值,即可得答案;
(2)①如图,连结BC,过点P作PE∥y轴,交BC于点E,根据B、C两点坐标可得直线BC的解析式,根据![]() 可求出OD、CD的长,设P(t,-t2+2t+3),则E(t,-t+3),可用含t的代数式表示出PE的长,根据S四边形CDBP=S△BCD+S△BPC可得S的表达式,根据二次函数的性质即可求出S的最大值;
可求出OD、CD的长,设P(t,-t2+2t+3),则E(t,-t+3),可用含t的代数式表示出PE的长,根据S四边形CDBP=S△BCD+S△BPC可得S的表达式,根据二次函数的性质即可求出S的最大值;
②由以CD为边,点C、D、Q、P为顶点的四边形是平行四边形可得PQ∥CD,且PQ=CD,分点P在点Q上方和点P在点Q下方两种情况,利用平行四边形的性质求出t值即可得答案.
(1)∵对称轴为x=1,A(-1,0),
∴B(3,0),
设所求抛物线的表达式为y=a(x+1)(x-3),
∵抛物线经过C(0,3)两点,
∴3=a(0+1)(0-3),
解得:a=-1,
∴所求抛物线的表达式为y=-(x+1)(x-3),即y=-x2+2x+3.
(2)①如图,连结BC,过点P作PE∥y轴,交BC于点E,
∵B(3,0),C(0,3),
∴直线BC的解析式为y=-x+3.
∵OB=3OD,OB=OC=3,
∴OD=1,CD=2.
设P(t,-t2+2t+3),则E(t,-t+3).
∴PE=-t2+2t+3-(-t+3)=-t2+3t.
∴S四边形CDBP=S△BCD+S△BPC=![]() CD·OB+
CD·OB+![]() PE·OB,
PE·OB,
∴S=![]()
![]()
![]()
∵a=![]() <0,且0<t<3,
<0,且0<t<3,
∴当t=![]() 时,S的最大值为
时,S的最大值为![]() .
.

②∵以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,
∴PQ∥CD,且PQ=CD=2,
∵点P在抛物线上,点Q在直线BC上,
∴点P(t,-t2+2t+3),点Q(t,-t+3).
分两种情况讨论:
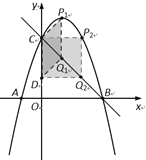
第一种情况:如图,当点P在点Q上方时,
∴(-t2+2t+3)-(-t+3)=2.即t2-3t+2=0,
解得:t1=1,t2=2,
∴P1(1,4),P2(2,3).
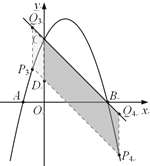
第二种情况:如图,当点P在点Q下方时,
∴(-t+3)-(-t2+2t+3)=2.即t2-3t-2=0,
解得:t3=![]() ,t4=
,t4=![]() ,
,
∴P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
综上所述,所有符合条件的点P的坐标分别为:P1(1,4), P2(2,3),P3(![]() ,
,![]() ), P4(
), P4(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 、
、![]() 是正方形与圆的另两个交点.
是正方形与圆的另两个交点.
(1)![]() __________
__________![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为__________;
的距离为__________;
(2)求![]() 的半径长和
的半径长和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
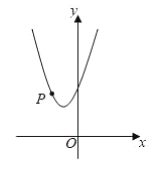
(1)求![]() 的值和图象的顶点坐标;
的值和图象的顶点坐标;
(2)点![]() 在该二次函数图象上.
在该二次函数图象上.
①当![]() 时,求
时,求![]() 的值;
的值;
②若点![]() 到
到![]() 轴的距离小于2,请根据图象直接写出
轴的距离小于2,请根据图象直接写出![]() 的取值范围;
的取值范围;
③直接写出点![]() 与直线
与直线![]() 的距离小于
的距离小于![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
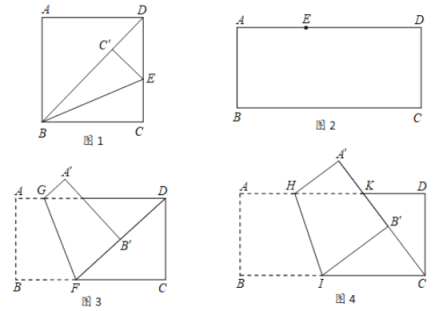
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=54°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.(画一画)如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段MN描清楚);
(3)(算一算)如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG=![]() ,求B'D的长;
,求B'D的长;
(4)(验一验)如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A',B'处,小明认为B'I所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
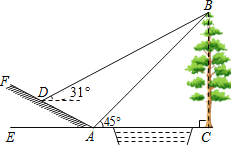
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了不完整的两种统计图:
四个等级,并绘制了不完整的两种统计图:
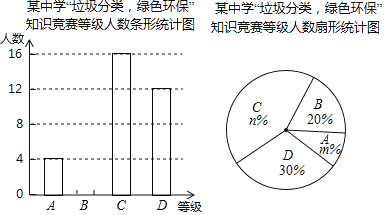
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有______人,并把条形统计图补充完整;
(2)扇形统计图中,![]() ______,
______,![]() ______,
______,![]() 等级对应的圆心角为______度;
等级对应的圆心角为______度;
(3)小明是四名获![]() 等级的学生中的一位,学校将从获
等级的学生中的一位,学校将从获![]() 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
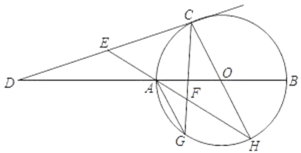
【题目】如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一点,过C点的切线与BA的延长线交于D点,E为CD上一点,连接EA并延长交⊙O于H,F为EH上一点,且EF=CE,CF交延长线交⊙O于G.
(1)求证:弧AG=弧GH;
(2)若E为DC的中点,sim∠CDO=![]() ,AH=2
,AH=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
(k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
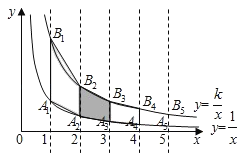
(1)用含k的代数式表示S1=_____.
(2)若S19=39,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com